55 The Basics of the Cost of Capital

Defining the Cost of Capital

Risk, return, and the time value of money are central inputs in distilling the cost of capital as an investor or borrower.

Learning Objectives

Understand the broader concepts in the cost of capital.

Key Takeaways

Key Points

  • Defining the cost of capital takes into account two general perspectives: the required rate of return of the lender and the weighted average cost of capital for the borrower.
  • Understanding the time value of money and understanding how to discount cash flows and returns into present value are important in assessing the cost of capital.
  • As an investor, understanding the opportunity cost of foregone investments as a result of risk and expected return is critical to intelligent investing.
  • By calculating and understanding the cost of debt and the cost of equity, organizations can calculate a weighted average cost of capital (WACC) consolidating all funding sources.
  • Ultimately the cost of capital accounts for opportunity cost, risk, return, and the time value of money.

Key Terms

  • risk-free rate: The default rate of return attached to a ‘risk free’ asset, such as a treasury bond. While nothing is completely risk free, these assets are as close to minimal risk as possible and represent the lowest practical rate of return.

When defining the cost of capital, it’s useful to frame it from either the borrower’s point of view (i.e. the organization) or the lender’s point of view (the investor). For the organization borrowing the capital, the cost of capital is the cumulative rate of interest (usually derived as an average rate, combining all capital inputs) applied to the borrowed capital to fund a project. From the investor’s point of view, the cost of capital is the relative required return rate considering the risk of the investment being made.

If this all sounds a bit confusing, don’t worry. Here’s an overview of the most important concepts:

Net Present Value (NPV)

The reason that capital incurs interest revolves around the simple fact that time has an impact on the valuation of capital, presenting opportunity costs and risk. To take into account the present value of future cash flows is therefore an important aspect of anticipating the rate of return on an investment. An NPV calculation will look at the forecasts for future cash flows, and discount those into present day dollars based on a given interest rate. This allows investors and organizations to determine if the cost of capital will be offset by the profits of a given investment.

Required Rate of Return

From the investor’s point of view, every investment has a required rate of return for (generally) two reasons: the opportunity cost of foregone investments and the risk of the borrower defaulting on payments. For example, if an investor can get 10% return on an investment with exactly the same risk as an option with 12% return, the investor would incur an opportunity cost of 2% by investing in the 10% return option. Similarly, if two investments both yield a 10% return but present different levels of risk, an investor would make the decision based on the lowest risk option.

Cost of Debt

As an organization, one of the options for sourcing capital is to pursue debt. This can either be through taking out a loan or putting selling corporate bonds. These options tend to have lower interest rates, and long payback periods. Debt is paid back first in the case of bankruptcy, lowering it’s risk as an investment (and subsequently, lowering it’s return). The cost of this capital is calculated as:

 

KD=(Rf+credit risk rate)(1−T){\displaystyle \text{K}_{\text{D}}=(\text{R}_{\text{f}}+{\text{credit risk rate}})(1-\text{T})} 

Rf is the risk-free rate and T is the corporate rate. Tax is included in debt as debt is discounted as a deductible expense.

Cost of Equity

Equity, usually represented as shares of stock, is another option for borrowing (and investing) at the organizational level. Equity’s cost is calculated via the capital asset pricing model (CAPM), as follows:

 

Es=Rf+βs(Rm−Rf){\displaystyle \text{E}_{\text{s}}=\text{R}_{\text{f}}+\beta _{\text{s}}(\text{R}_{\text{m}}-\text{R}_{\text{f}})} 

The variables above are:

  • Es is the expected return for a security
  • Rf is the expected risk-free rate
  • βs is the sensitivity to market risk
  • Rm is the historical return of the market
  • (Rm – Rf) is the risk premium compared to the risk-free rate

Weighted Average Cost of Capital

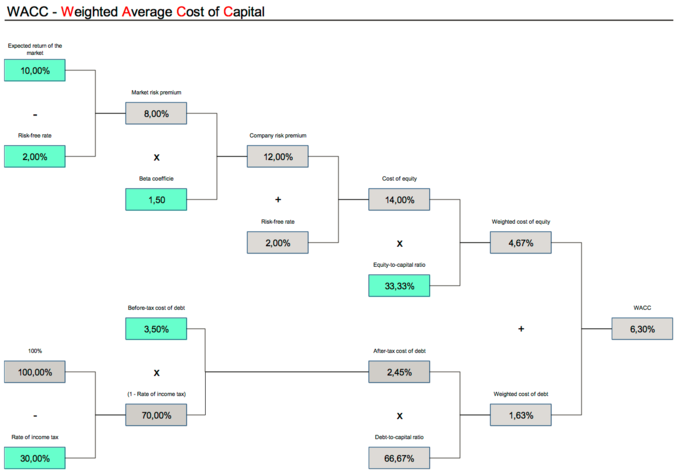
With the above options in mind, the weighted average cost of capital (WACC) normalizes the cost of capital by combining the interest rates being incurred from both debt and equity. It can be written as:

 

WACC=DD+EKd+ED+EKe{\displaystyle {\text{WACC}}={\frac {\text{D}}{\text{D}+\text{E}}}\text{K}_{\text{d}}+{\frac {\text{E}}{\text{D}+\text{E}}}\text{K}_{\text{e}}}​

While each of these concepts is quite a bit more complex in implementation, this overview gives some scope as to the general definition and considerations involved in the cost of capital. Capital incurs costs due to risk, return, and the intrinsic time value of money.

Differences Between Required Return and the Cost of Capital

The average cost of capital is calculated via combining the overall average required rate on debt stakeholders and equity stakeholders

Learning Objectives

Calculate the weighted average cost of capital by understanding the required rate of various investors.

Key Takeaways

Key Points

  • Investors need to know the overall required return based on the risk of the investment in order to compare this to other investment opportunities.
  • The overall cost of capital will be the combination of various required rates of returns on behalf of investors, some of which will likely be debt while others will be equity.
  • The cost of capital should be weighted in order for the overall weight average cost of capital (WACC) for a given project or venture to be calculated. This WACC determines the overall required return on the project to become profitable (or at least break even).
  • As a result, the difference between required return and cost of capital is twofold: the perspective (i.e. the borrower or the lender) and the potential for averaging these costs of capital from the borrowers perspective (i.e. multiple required returns).

Key Terms

  • weighted average cost of capital: Or WACC, this is a calculation of the various required returns on a project, which ultimately determines the profitability required to break even.

Why Require Return Rates

When making investments on the business level, it is critical to create a required amount of return on the project. A required return is exactly what it sounds like— the amount of profit as a percentage of the investment that will be created over a given time period.

As an investor, this required rate is a practical concept. Investors have options, and each of those options will offer a rate of return. The risk attached to those rates will fluctuate, as higher risk projects require a higher rate of return. Through establishing this required rate, the investor is stipulating their expectations on repayment of this invested capital, which the borrower will confirm and agree to repay over a set time period (usually via timed installments).

So What’s Cost of Capital?

This required amount of return will ultimately equal the cost of capital, as the required rate from the investor is now a cost being put on the borrower. Now, cost of capital for a given investor will always equate to the required return. However, things get a bit more complicated when organizations fund new projects via a wide variety of stakeholders.

Weighted Average Cost of Capital (WACC)

This is where the concept of weighted average cost of capital (WACC) enters the equation, as there may be more than one investor with varying rates of return. Intuitively, the WACC will then be a calculation which takes into account the percentage of the overall borrowed capital that each form of investment contributed, and the respective required rates. To make this a bit clearer, let’s look at the equation of WACC that takes into account one rate for equity and another rate for debt:

 

WACC=DD+EKd+ED+EKe{\displaystyle {\text{WACC}}={\frac {\text{D}}{\text{D}+\text{E}}}\text{K}_{\text{d}}+{\frac {\text{E}}{\text{D}+\text{E}}}\text{K}_{\text{e}}}​

In the above equation, you have D as total debt, E as total equity, Kd as the required return on debt, and Ke as the required return on equity. If various investors require different rates of return, the equation can be altered accordingly (i.e. Kd and Ke will each be averaged based on their respective inputs). For the sake of simplicity, this WACC equation will suffice for the majority of calculations.

 

While this image goes into a bit more detail on the derivation of the cost of equity and the cost of debt, the final 3 boxes on the right ultimately demonstrate the way in which required rates balance out into a WACC (one for debt, one for equity).
WACC: While this image goes into a bit more detail on the derivation of the cost of equity and the cost of debt, the final three boxes on the right ultimately demonstrate the way in which required rates balance out into a WACC (one for debt, one for equity). Debt tends to be a lower rate because it is paid out first if a company goes bankrupt (i.e. lower risk). Equity is a bit higher risk (only paid out if there is capital remaining after debts are paid), and thus equity has a higher rate (and higher risk).

The Difference

Ultimately, the difference between the cost of capital and the required return is both one of perspective (borrower looks at cost of capital for a project; investors look at required return) as well as the potential for a WACC, which integrates various required returns for a single investment project.

Relationship Between Financial Policy and the Cost of Capital

Financial policy, not cost of capital, must be utilized to determine which investments to pursue, given that resources are limited.

Learning Objectives

Explain the relationship between a company’s financial policy and its cost of capital.

Key Takeaways

Key Points

  • As opposed to strictly using cost of capital, decisions must be made using opportunity cost of capital.
  • Opportunity cost of capital is the amount of money foregone by investing in one asset compared to another.
  • Facets of financial policy include valuation, portfolio theory, hedging, and capital structure.

Key Terms

  • leverage: The use of borrowed funds with a contractually determined return to increase the ability of a business to invest and earn an expected higher return (usually at high risk).

Financial Policy and the Cost of Capital

Financial policy is used by companies or investors in order to determine the best way to allocate their resources. In regard to cost of capital, financial policy must be utilized in order to decide which investments have the highest return, given that resources are limited. To analyze various options, managers use valuation techniques, such as the capital asset pricing model or discounted cash flow analysis. As opposed to strictly using cost of capital, decisions must be made using opportunity cost of capital.

Opportunity cost of capital is the amount of money foregone by investing in one asset compared to another. As an investor, this can simply be a choice of one asset over another. As a company, this choice can also involve the use of current assets in new investments. For example, an idle piece of land could be used for a new factory; however, the opportunity cost of what else it could have been used for must be taken into consideration during analysis.

Other Roles of Financial Policy

The use of financial policy in decision making does not only involve valuation. Other facets include portfolio theory, hedging, and capital structure.

Oil Prices: Companies often use hedging techniques to offset price fluctuations for commodities. The fluctuation of oil prices can be seen in the above graph
Oil Prices: Companies often use hedging techniques to offset price fluctuations for commodities. The fluctuation of oil prices can be seen in the above graph.

Portfolio Theory

Portfolio theory is a mathematical formulation of the concept of diversification in investing. It attempts to maximize the expected return of a portfolio, or a collection of investments, for a given amount of risk by carefully choosing the proportions of various assets. In other terms, portfolio theory attempts to minimize risk for a given level of expected return. For example, to the extent prices in the stock market move differently from prices in the bond market, a collection of both types of assets can, in theory, face lower overall risk than either could individually.

Hedging

Along the same lines, companies use hedging techniques to offset potential gains and losses. Hedging is the practice of taking a position in one market to offset and balance against the risk adopted by assuming a position in a contrary or opposing market or investment. Simply put, a hedge is used to reduce any substantial gains or losses suffered by an individual or an organization. Companies often use hedging techniques to offset the risk of price fluctuation for commodities, such as oil or agricultural products.

Capital Structure

The capital structure of a company refers to the way it finances its assets through some combination of equity, debt, or hybrid securities. Capital structure may be highly complex and include dozens of sources. A simple example, though, would be a company that sold $20 million in equity and $80 million in debt. This company would be 20% equity financed and 80% debt financed. A company’s ratio of debt to total financing is referred to as its leverage.

Licenses and Attributions

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

PPSC FIN 2010 Principles of Finance by Cristal Brietbeil and Eric Schroeder is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book