99 13.1 The Hydrological Cycle — Physical Geology – 2nd Edition
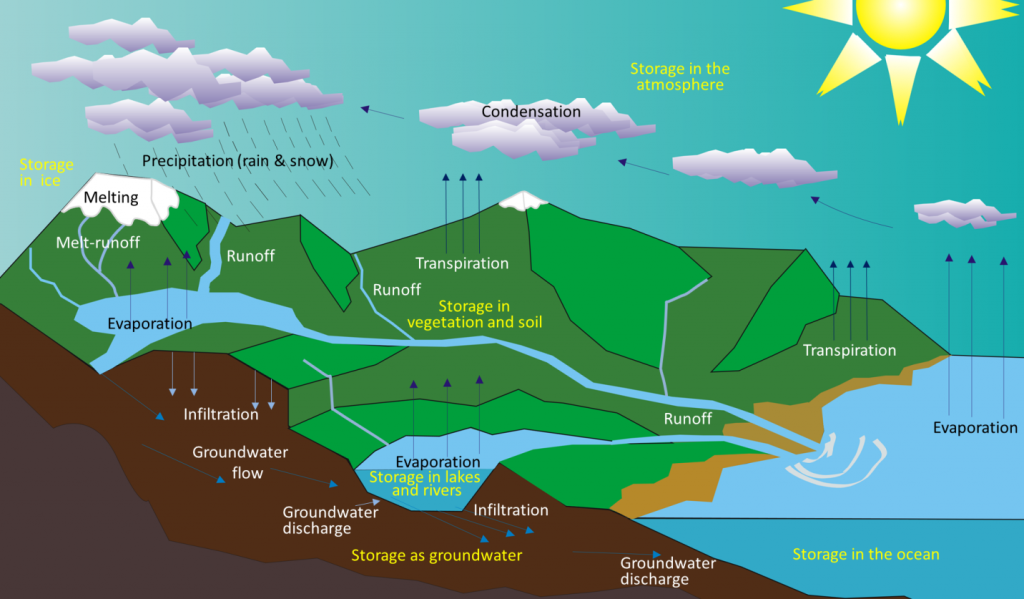

Even while it’s moving around, water is stored in various reservoirs. The largest, by far, is the oceans, accounting for 97% of the volume. Of course, that water is salty. The remaining 3% is fresh water. Two-thirds of our fresh water is stored in ice and one-third is stored in the ground. The remaining fresh water—about 0.03% of the total—is stored in lakes, streams, vegetation, and the atmosphere. To put that in perspective, let’s imagine putting all of Earth’s water into a 1 litre jug (Figure 13.1.2). We start by almost filling the jug with 970 millilitres of water and 34 grams of salt. Then we add one regular-sized (roughly 20 millilitres) ice cube (representing glacial ice) and two teaspoons (roughly 10 millilitres) of groundwater. All of the water that we see around us in lakes and streams and up in the sky can be represented by adding three more drops from an eyedropper.
Although the proportion of Earth’s water that is in the atmosphere is tiny, the actual volume is huge. At any given time, there is the equivalent of approximately 13,000 cubic kilometres (km3) of water in the air in the form of water vapour and water droplets in clouds. Water is evaporated from the oceans, vegetation, and lakes at a rate of 1,580 km3 per day, and just about exactly the same volume falls as rain and snow every day—over both the oceans and land. The precipitation that falls on land goes back to the ocean in the form of stream flow (117 km3/day) and groundwater flow (6 km3/day). Most of the rest of this chapter is about that 117 km3/day of streamflow. The average discharge of the Fraser River into the ocean is approximately 0.31 km3/day, or 0.26% of the total flow of all rivers.
The residence time of a water molecule in the atmosphere (or any of the other reservoirs) can be estimated by dividing the amount that is there by the rate at which it is transferred in and out. For the atmosphere, we know that the reservoir size is 13,000 km3, and the rate of flux is 1,580 km3 per day. That’s the amount that goes into or comes out of the atmosphere in a day. If we divide 13,000 by 1,580, we get 8.22 days. This means that, on average, a molecule of water stays in the atmosphere for just over eight days. “Average” needs to be emphasized here because obviously some molecules stay in the air for only a few hours, while others may stay up there for weeks.
The volume of the oceans is 1,338,000,000 km3 and the flux rate is approximately the same (1,580 km3 per day). What is the average residence time of a water molecule in the ocean?
See Appendix 3 for Exercise 13.1 answers.
Media Attributions
- Figure 13.1.1: “Water Cycle Blank” © Ingwik. Adapted by Steven Earle. CC BY-SA.
- Figure 13.1.2: © Steven Earle. CC BY. Based on data from The Water Cycle: Freshwater Storage.
<!– pb_fixme –>
<!– pb_fixme –>

