9.4: Confidence Intervals for Means

Colorado Online

9.4: Confidence Intervals for Means

Learning Objectives

Explain what a confidence interval represents and determine how changes in sample size and confidence level affect the precision of the confidence interval.
Find confidence intervals for the population mean and the population proportion (when certain conditions are met), and perform sample size calculations.

Overview

As we mentioned in the introduction to interval estimation, we start by discussing interval estimation for the population mean μ. Here is a quick overview of how we introduce this topic.

Learn how a 95% confidence interval for the population mean μ is constructed and interpreted.
Generalize to confidence intervals with other levels of confidence (for example, what if we want a 99% confidence interval?).
Understand more broadly the structure of a confidence interval and the importance of the margin of error.
Understand how the precision of interval estimation is affected by the confidence level and sample size.
Learn under which conditions we can safely use the methods that are introduced in this section.

Recall the IQ example:

Example

Suppose that we are interested in studying the IQ levels of students at Smart University (SU). In particular (since IQ level is a quantitative variable), we are interested in estimating μ, the mean IQ level of all the students at SU.

We will assume that from past research on IQ scores in different universities, it is known that the IQ standard deviation in such populations is $σ = 15$ . In order to estimate μ , a random sample of 100 SU students was chosen, and their (sample) mean IQ level is calculated (let’s not assume, for now, that the value of this sample mean is 115, as before).

A large circle represents the Population of all Students at SU. We are interested in the variable IQ, and the unknown parameter is μ, the population mean IQ level. In addition, we know that σ = 15. From this population we create a sample of size n=100, represented by a smaller circle. In this sample, we need to find x bar We will now show the rationale behind constructing a 95% confidence interval for the population mean μ.

* We learned in the “Sampling Distributions” module of probability that according to the central limit theorem, the sampling distribution of the sample mean $¯ ¯ ¯ X$ is approximately normal with a mean of μ and standard deviation of $\frac{σ}{\sqrt{n}}$ . In our example, then, (where $σ = 15$ and n=100), the possible values of $¯ ¯ ¯ X$ , the sample mean IQ level of 100 randomly chosen students, is approximately normal, with mean μ and standard deviation $\frac{15}{\sqrt{100}} = 1.5$ .

* Next, we recall and apply the Standard Deviation Rule for the normal distribution, and in particular its second part:

There is a 95% chance that the sample mean we get in our sample falls within 2 * 1.5 = 3 of μ.

A distribution curve with a horizontal axis labeled "X bar." The curve is centered at X-bar=μ, and marked on the axis is μ+3 and μ-3. There is a 95% chance that any x-bar will fall between μ-3 and μ+3.

* Obviously, if there is a certain distance between the sample mean and the population mean, we can describe that distance by starting at either value. So, if the sample mean ( $¯ x$ ) falls within a certain distance of the population mean μ, then the population mean μ falls within the same distance of the sample mean.

Therefore, the statement, “There is a 95% chance that the sample mean $¯ x$ falls within 3 units of μ” can be rephrased as: “We are 95% confident that the population mean μ falls within 3 units of $¯ x$ .”

So, if we happen to get a sample mean of $¯ x = 115$ , then we are 95% sure that μ falls within 3 of 115, or in other words that μ is covered by the interval (115 – 3, 115 + 3) = (112,118).

(On later pages, we will use similar reasoning to develop a general formula for a confidence interval.)

Comment

Note that the first phrasing is about $¯ x$ , which is a random variable; that’s why it makes sense to use probability language. But the second phrasing is about μ, which is a parameter, and thus is a “fixed” value that doesn’t change, and that’s why we shouldn’t use probability language to discuss it. This point will become clearer after you do the activities on the next page.

The General Case

Let’s generalize the IQ example. Suppose that we are interested in estimating the unknown population mean (μ) based on a random sample of size n. Further, we assume that the population standard deviation (σ) is known.

A large circle represents the population of interest. μ is unknown, but σ is known about the population. From the population we create a SRS of size n, represented by a smaller circle. We can find x-bar for this SRS.

The values of $¯ x$ follow a normal distribution with (unknown) mean μ and standard deviation $\frac{σ}{\sqrt{n}}$ (known, since both σ and n are known). By the (second part of the) Standard Deviation Rule, this means that:

There is a 95% chance that our sample mean ( $¯ x$ ) will fall within $2 * \frac{σ}{\sqrt{n}}$ of μ,

which means that:

We are 95% confident that μ falls within $2 * \frac{σ}{\sqrt{n}}$ of our sample mean ( $¯ x$ ).

Or, in other words, a 95% confidence interval for the population mean μ is:

$(¯ x - 2 * \frac{σ}{\sqrt{n}}, ¯ x + 2 * \frac{σ}{\sqrt{n}})$

Here, then, is the general result:

Suppose a random sample of size n is taken from a normal population of values for a quantitative variable whose mean (μ) is unknown, when the standard deviation (σ) is given. A 95% confidence interval (CI) for μ is:

$¯ x \pm 2 * \frac{σ}{\sqrt{n}}$

Comment

Note that for now we require the population standard deviation (σ) to be known. Practically, σ is rarely known, but for some cases, especially when a lot of research has been done on the quantitative variable whose mean we are estimating (such as IQ, height, weight, scores on standardized tests), it is reasonable to assume that σ is known. Eventually, we will see how to proceed when σ is unknown, and must be estimated with sample standard deviation (s).

Let’s look at another example.

Example

An educational researcher was interested in estimating μ, the mean score on the math part of the SAT (SAT-M) of all community college students in his state. To this end, the researcher has chosen a random sample of 650 community college students from his state, and found that their average SAT-M score is 475. Based on a large body of research that was done on the SAT, it is known that the scores roughly follow a normal distribution with the standard deviation $σ = 100$ .

Here is a visual representation of this story, which summarizes the information provided:

A large circle represents the population of Community college students in the researcher's state. μ is unknown, but σ is known about the population. From the population we create a SRS of size n=650, represented by a smaller circle. We can find that x-bar=475 for this SRS.

Based on this information, let’s estimate μ with a 95% confidence interval.

Using the formula we developed before, $¯ x \pm 2 * \frac{σ}{\sqrt{n}}$ , a 95% confidence interval for μ is:

$(475 - 2 * \frac{100}{\sqrt{650}}, 475 + 2 * \frac{100}{\sqrt{650}})$ , which is (475 – 7.8 , 475 + 7.8) = (467.2, 482.8). In this case, it makes sense to round, since SAT scores can be only whole numbers, and say that the 95% confidence interval is (467, 483).

We are not done yet. An equally important part is to interpret what this means in the context of the problem.

We are 95% confident that the mean SAT-M score of all community college students in the researcher’s state is covered by the interval (467, 483). Note that the confidence interval was obtained by taking $475 \pm 8$ (rounded). This means that we are 95% confident that by using the sample mean ( $¯ x = 475$ ) to estimate μ, our error is no more than 8.

We just saw that one interpretation of a 95% confidence interval is that we are 95% confident that the population mean (μ) is contained in the interval. Another useful interpretation in practice is that, given the data, the confidence interval represents the set of plausible values for the population mean μ.

Example

As an illustration, let’s return to the example of mean SAT-Math score of community college students. Recall that we had constructed the confidence interval (467, 483) for the unknown mean SAT-M score for all community college students.

Here is a way that we can use the confidence interval:

Do the results of this study provide evidence that μ, the mean SAT-M score of community college students, is lower than the mean SAT-M score in the general population of college students in that state (which is 480)?

The 95% confidence interval for μ was found to be (467, 483). Note that 480, the mean SAT-M score in the general population of college students in that state, falls inside the interval, which means that it is one of the plausible values for μ.

A number line, on which the 95% confidence interval for μ has been marked, from 467 to 483. At 480 is the mean SAT-M score in the general population of college students in the state.

This means that μ could be 480 (or even higher, up to 483), and therefore we cannot conclude that the mean SAT-M score among community college students in the state is lower than the mean in the general population of college students in that state. (Note that the fact that most of the plausible values for μ fall below 480 is not a consideration here.)

Comment

Recall that in the formula for the 95% confidence interval for μ, $¯ x \pm 2 * \frac{σ}{\sqrt{n}}$ , the 2 comes from the Standard Deviation Rule, which says that any normal random variable (in our case $¯ ¯ ¯ X$ ), has a 95% chance (or probability of 0.95) of taking a value that is within 2 standard deviations of its mean.

As you recall from the discussion about the normal random variable, this is only an approximation, and to be more accurate, there is a 95% chance that a normal random variable will take a value within 1.96 standard deviations of its mean. Therefore, a more accurate formula for the 95% confidence interval for μ is $¯ x \pm 1.96 * \frac{σ}{\sqrt{n}}$ , which you’ll find in most introductory statistics books. In this course, we’ll use 2 (and not 1.96), which is close enough for our purposes.

Other Levels of Confidence

The most commonly used level of confidence is 95%. However, we may wish to increase our level of confidence and produce an interval that is almost certain to contain μ. Specifically, we may want to report an interval for which we are 99% confident—rather than only 95% confident—that it contains the unknown population mean.

Using the same reasoning as in the last comment, in order to create a 99% confidence interval for μ, we should ask: There is a probability of 0.99 that any normal random variable takes values within how many standard deviations of its mean? The precise answer is 2.576, and therefore, a 99% confidence interval for μ is $¯ x \pm 2.576 * \frac{σ}{\sqrt{n}}$ .

Another commonly used level of confidence is a 90% level of confidence. Since there is a probability of 0.90 that any normal random variable takes values within 1.645 standard deviations of its mean, the 90% confidence interval for μ is $¯ x \pm 1.645 * \frac{σ}{\sqrt{n}}$ .

Example

Let’s go back to our first example, the IQ example:

The IQ level of students at a particular university has an unknown mean, μ, and a known standard deviation, $σ = 15$ . A simple random sample of 100 students is found to have a sample mean IQ, $¯ x = 115$ . Estimate μ with 90%, 95%, and 99% confidence intervals.

A 90% confidence interval for μ is $¯ x \pm 1.645 \frac{σ}{\sqrt{n}} = 115 \pm 1.645 (\frac{15}{\sqrt{100}}) = 115 \pm 2.5 = (112.5, 117.5)$ .

A 95% confidence interval for μ is $¯ x \pm 2 \frac{σ}{\sqrt{n}} = 115 \pm 2 (\frac{15}{\sqrt{100}}) = 115 \pm 3.0 = (112, 118)$ .

A 99% confidence interval for μ is $¯ x \pm 2.576 \frac{σ}{\sqrt{n}} = 115 \pm 2.576 (\frac{15}{\sqrt{100}}) = 115 \pm 4.0 = (111, 119)$ .

The 99% confidence interval is wider than the 95% confidence interval, which is wider than the 90% confidence interval.

A number line illustrating confidence intervals for μ. x-bar is marked at 115. The interval 112.5 and 117.5 is the 90% confidence interval. Enclosing this interval is the interval 112 and 118, which is the 95% confidence interval. Even larger is the 99% confidence interval, ranging from 111 to 119.

This is not very surprising, given that in the 99% interval we multiply the standard deviation by 2.576, in the 95% by 2, and in the 90% only by 1.645. Beyond this numerical explanation, there is a very clear intuitive explanation and an important implication of this result.

Let’s start with the intuitive explanation. The more certain I want to be that the interval contains the value of μ, the more plausible values the interval needs to include in order to account for that extra certainty. I am 95% certain that the value of μ is one of the values in the interval (112,118). In order to be 99% certain that one of the values in the interval is the value of μ, I need to include more values, and thus provide a wider confidence interval.

In our example, the wider 99% confidence interval (111, 119) gives us a less precise estimation about the value of μ than the narrower 90% confidence interval (112.5, 117.5), because the smaller interval “narrows in” on the plausible values of μ.

The important practical implication here is that researchers must decide whether they prefer to state their results with a higher level of confidence or produce a more precise interval. In other words,

There is a trade-off between the level of confidence and the precision with which the parameter is estimated.

The price we have to pay for a higher level of confidence is that the unknown population mean will be estimated with less precision (i.e., with a wider confidence interval). If we would like to estimate μ with more precision (i.e., a narrower confidence interval), we will need to sacrifice and report an interval with a lower level of confidence.

So far, we’ve developed the confidence interval for the population mean from scratch, based on results from probability, and discussed the trade-off between the level of confidence and the precision of the interval. The price you pay for a higher level of confidence is a lower level of precision of the interval (i.e., a wider interval).

Is there a way to bypass this trade-off? In other words, is there a way to increase the precision of the interval (i.e., make it narrower) without compromising on the level of confidence? We will answer this question shortly, but first we need to get a deeper understanding of the different components of the confidence interval and its structure.

Understanding the general structure of the confidence intervals

We explored the confidence interval for μ for different levels of confidenceand found that, in general, it has the following form:

$¯ x \pm z^{*} \cdot \frac{σ}{\sqrt{n}}$ ,

where z* is a general notation for the multiplier that depends on the level of confidence. As we discussed before:

For a 90% level of confidence, z* = 1.645

For a 95% level of confidence, z* = 2 (or 1.96 if you want to be really precise)

For a 99% level of confidence, z* = 2.576

To start our discussion about the structure of the confidence interval, let’s denote the $z^{*} \cdot \frac{σ}{\sqrt{n}}$ formula by m.

The confidence interval, then, has the form: $¯ x \pm m$ :

A formula: x-bar ± z-star × σ/√n Note that z-star × σ/√n is m.

$¯ x$ is the sample mean, the point estimator for the unknown population mean (μ).

m is called the margin of error, since it represents the maximum estimation error for a given level of confidence.

For example, for a 95% confidence interval, we are 95% sure that our estimate will not depart from the true population mean by more than m, the margin of error.

m is further made up of the product of two components:

z*, the confidence multiplier, and

$\frac{σ}{\sqrt{n}}$ , which is the standard deviation of $¯ ¯ ¯ X$ , the point estimator of μ.

Here is a summary of the different components of the confidence interval and its structure:

x-bar is the point estimator. It is either added to or subtracted by the margin of error (m). The margin of error is composed of the confidence multiplier, z-star, which is multiplied by the standard deviation of the point estimator, which is σ/√n .

This structure:

$estimate \pm margin of error$ ,

where the margin of error is further composed of the product of a confidence multiplier and the standard deviation (or, as we’ll see, the standard error) is the general structure of all confidence intervals that we will encounter in this course.

Obviously, even though each confidence interval has the same components, what these components actually are is different from confidence interval to confidence interval, depending on what unknown parameter the confidence interval aims to estimate.

Since the structure of the confidence interval is such that it has a margin of error on either side of the estimate, it is centered at the estimate (in our case, $¯ x$ ), and its width (or length) is exactly twice the margin of error:

A number line, on which the estimate has been placed. To the left and to the right are two intervals with the size m. So, the confidence interval, which comprises of both margins of errors (the left one and right one) is of width 2m.

The margin of error, m, is therefore “in charge” of the width (or precision) of the confidence interval, and the estimate is in charge of its location (and has no effect on the width).

Let us now go back to the confidence interval for the mean, and more specifically, to the question that we posed at the beginning of the previous page:

Is there a way to increase the precision of the confidence interval (i.e., make it narrower) without compromising on the level of confidence?

Since the width of the confidence interval is a function of its margin of error, let’s look closely at the margin of error of the confidence interval for the mean and see how it can be reduced:

$z^{*} * \frac{σ}{\sqrt{n}}$

Since z* controls the level of confidence, we can rephrase our question above in the following way:

Is there a way to reduce this margin of error other than by reducing z*?

If you look closely at the margin of error, you’ll see that the answer is yes. We can do that by increasing the sample size n (since it appears in the denominator).

Exercise

Confidence Intervals for the Population Mean

Let’s look at an example first and then explain why increasing the sample size is a way to increase the precision of the confidence interval without compromising on the level of confidence.

Example

Recall the IQ example:

The IQ level of students at a particular university has an unknown mean (μ) and a known standard deviation of $σ = 15$ . A simple random sample of 100 students is found to have the sample mean IQ $¯ x = 115$ . A 95% confidence interval for μ in this case is:

$¯ x \pm 2 \frac{σ}{\sqrt{n}} = 115 \pm 2 (\frac{15}{\sqrt{100}}) = 115 \pm 3.0 = (112, 118)$

Note that the margin of error is m = 3, and therefore the width of the confidence interval is 6.

Now, what if we change the problem slightly by increasing the sample size, and assume that it was 400 instead of 100?

A large circle represents the Population of all Students at SU. We are interested in the variable IQ, and the unknown parameter is μ, the population mean IQ level. In addition, we know that σ = 15. From this population we create a sample of size n=400, represented by a smaller circle. In this sample, we find that x bar = 115.

In this case, the 95% confidence interval for μ is:

$¯ x \pm 2 \frac{σ}{\sqrt{n}} = 115 \pm 2 (\frac{15}{\sqrt{400}}) = 115 \pm 1.5 = (113.5, 116.5)$

The margin of error here is only m = 1.5, and thus the width is only 3.

Note that for the same level of confidence (95%) we now have a narrower, and thus more precise, confidence interval.

Let’s try to understand why a larger sample size will reduce the margin of error for a fixed level of confidence. There are three ways to explain it: mathematically, using probability theory, and intuitively.

We’ve already alluded to the mathematical explanation; the margin of error is $z^{*} * \frac{σ}{\sqrt{n}}$ , and since n, the sample size, appears in the denominator, increasing n will reduce the margin of error.

As we saw in our discussion about point estimates, probability theory tells us that

Two sampling distribution curves for x-bar. One is squished down and wider, while the other is much taller and narrower. Both curves share the same μ. The tall, narrow distribution was based on a larger sample size, which has a smaller standard deviation, and so is less spread out. This means that values of x-bar are more likely to be closer to μ when the sample size is larger.

This explains why with a larger sample size the margin of error (which represents how far apart we believe $¯ x$ might be from μ for a given level of confidence) is smaller.

On an intuitive level, if our estimate $¯ x$ is based on a larger sample (i.e., a larger fraction of the population), we have more faith in it, or it is more reliable, and therefore we need to account for less error around it.

Comment

While it is true that for a given level of confidence, increasing the sample size increases the precision of our interval estimation, in practice, increasing the sample size is not always possible. Consider a study in which there is a non-negligible cost involved for collecting data from each participant (an expensive medical procedure, for example). If the study has some budgetary constraints, which is usually the case, increasing the sample size from 100 to 400 is just not possible in terms of cost-effectiveness. Another instance in which increasing the sample size is impossible is when a larger sample is simply not available, even if we had the money to afford it. For example, consider a study on the effectiveness of a drug on curing a very rare disease among children. Since the disease is rare, there are a limited number of children who could be participants. This is the reality of statistics. Sometimes theory collides with reality, and you just do the best you can.

Sample Size Calculations

As we just learned, for a given level of confidence, the sample size determines the size of the margin of error and thus the width, or precision, of our interval estimation. This process can be reversed.

In situations where a researcher has some flexibility as to the sample size, the researcher can calculate in advance what the sample size is that he/she needs in order to be able to report a confidence interval with a certain level of confidence and a certain margin of error. Let’s look at an example.

Example

Recall the example about the SAT-M scores of community college students.

An educational researcher is interested in estimating μ, the mean score on the math part of the SAT (SAT-M) of all community college students in his state. To this end, the researcher has chosen a random sample of 650 community college students from his state, and found that their average SAT-M score is 475. Based on a large body of research that was done on the SAT, it is known that the scores roughly follow a normal distribution, with the standard deviation $σ = 100$ .

The 95% confidence interval for μ is $(475 - 2 * \frac{100}{\sqrt{650}}, 475 + 2 * \frac{100}{\sqrt{650}})$ , which is roughly $475 \pm 8$ , or (467,484). For a sample size of n = 650, our margin of error is 8.

Now, let’s think about this problem in a slightly different way:

An educational researcher is interested in estimating μ, the mean score on the math part of the SAT (SAT-M) of all community college students in his state with a margin of error of (only) 5, at the 95% confidence level. What is the sample size needed to achieve this? (σ, of course, is still assumed to be 100).

To solve this, we set:

$m = 2 \cdot \frac{100}{\sqrt{n}} = 5$

so

$\sqrt{n} = \frac{2 (100)}{5}$

and

$n = {(\frac{2 (100)}{5})}^{2} = 1600$

So, for a sample size of 1,600 community college students, the researcher will be able to estimate μ with a margin of error of 5, at the 95% level. In this example, we can also imagine that the researcher has some flexibility in choosing the sample size, since there is a minimal cost (if any) involved in recording students’ SAT-M scores, and there are many more than 1,600 community college students in each state.

Rather than take the same steps to isolate n every time we solve such a problem, we may obtain a general expression for the required n for a desired margin of error m and a certain level of confidence.

Since $m = z * \frac{σ}{\sqrt{n}}$ is the formula to determine m for a given n, we can use simple algebra to express n in terms of m (multiply both sides by the square root of n, divide both sides by m, and square both sides) to get

$n = {(\frac{^{*} σ}{m})}^{2}$ .

Comment

Clearly, the sample size n must be an integer. In the previous example we got n = 1,600, but in other situations, the calculation may give us a non-integer result. In these cases, we should always round up to the next highest integer.

Using this “conservative approach,” we’ll achieve an interval at least as narrow as the one desired.

Example

IQ scores are known to vary normally with a standard deviation of 15. How many students should be sampled if we want to estimate the population mean IQ at 99% confidence with a margin of error equal to 2?

$n = {(\frac{^{*} σ}{m})}^{2} = {(\frac{2.576 (15)}{2})}^{2} = 373.26$

Round up to be safe, and take a sample of 374 students.

We are almost done with this section. We need to discuss just a few more questions:

Is it always okay to use the confidence interval we developed for μ when σ is known?
What if σ is unknown?
How can we use statistical software to calculate confidence intervals for us?

When Is It Safe to Use the Confidence Interval We Developed?

One of the most important things to learn with any inference method is the conditions under which it is safe to use it. It is very tempting to apply a certain method, but if the conditions under which this method was developed are not met, then using this method will lead to unreliable results, which can then lead to wrong and/or misleading conclusions. As you’ll see throughout this section, we always discuss the conditions under which each method can be safely used.

In particular, the confidence interval for μ (when σ is known), $¯ x \pm z^{*} * \frac{σ}{\sqrt{n}}$ , was developed assuming that the sampling distribution of $¯ ¯ ¯ X$ is normal; in other words, that the Central Limit Theorem applies. In particular, this allowed us to determine the values of z*, the confidence multiplier, for different levels of confidence.

First, the sample must be random. Assuming that the sample is random, recall from the Probability unit that the Central Limit Theorem works when the sample size is large (a common rule of thumb for “large” is n > 30), or, for smaller sample sizes, if it is known that the quantitative variable of interest is distributed normally in the population. The only situation in which we cannot use the confidence interval, then, is when the sample size is small and the variable of interest is not known to have a normal distribution. In that case, other methods, called nonparametric methods, which are beyond the scope of this course, need to be used. This can be summarized in the following table:

Exercise

Confidence Intervals for the Population Mean

What if σ is unknown?

As we discussed earlier, when variables have been well-researched in different populations it is reasonable to assume that the population standard deviation (σ) is known. However, this is rarely the case. What if σ is unknown?

Well, there is some good news and some bad news.

The good news is that we can easily replace the population standard deviation, σ, with the sample standard deviation, s.

A large circle represents the population of interest. μ is unknown and σ is unknown. From the population we create a SRS of size n, represented by a smaller circle. We can find x-bar for this SRS, and we can also obtain S. We use this instead of the unknown σ.

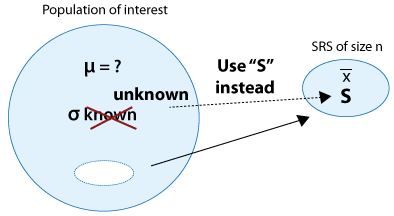
The bad news is that once σ has been replaced by s, we lose the Central Limit Theorem, together with the normality of $¯ ¯ ¯ X$ , and therefore the confidence multipliers z* for the different levels of confidence (1.645, 2, 2.576) are (generally) not accurate any more. The new multipliers come from a different distribution called the “t distribution” and are therefore denoted by t* (instead of z*). We will discuss the t distribution in more detail when we talk about hypothesis testing.

The confidence interval for the population mean (μ) when (σ) is unknown is therefore:

$¯ x \pm t^{*} * \frac{s}{\sqrt{n}}$

(Note that this interval is very similar to the one when σ is known, with the obvious changes: s replaces σ, and t* replaces z* as discussed above.)

There is an important difference between the confidence multipliers we have used so far (z*) and those needed for the case when σ is unknown (t*). Unlike the confidence multipliers we have used so far (z*), which depend only on the level of confidence, the new multipliers (t*) have the added complexity that they depend on both the level of confidence and on the sample size (for example, the t* used in a 95% confidence when n = 10 is different from the t* used when n = 40). Due to this added complexity in determining the appropriate t*, we will rely heavily on software in this case.

Comments

1. Since it is quite rare that σ is known, this interval (sometimes called a one-sample t confidence interval) is more commonly used as the confidence interval for estimating μ. (Nevertheless, we could not have presented it without our extended discussion up to this point, which also provided you with a solid understanding of confidence intervals.)

2. The quantity $\frac{s}{\sqrt{n}}$ is called the standard error of $¯ ¯ ¯ X$ . The central limit theorem tells us that $\frac{σ}{\sqrt{n}}$ is the standard deviation of $¯ ¯ ¯ X$ (and this is the quantity used in confidence interval when σ is known). In general, whenever we replace parameters with their sample counterparts in the standard deviation of a statistic, the resulting quantity is called the standard error of the statistic. In this case, we replaced σ with its sample counterpart (s), and thus $\frac{s}{\sqrt{n}}$ is the standard error of (the statistic) $¯ ¯ ¯ X$ .

3. As before, to safely use this confidence interval, the sample must be random, and the only case when this interval cannot be used is when the sample size is small and the variable is not known to vary normally.

Final comment

It turns out that for large values of n, the t* multipliers are not that different from the z* multipliers, and therefore using the interval formula:

$¯ x \pm z^{*} * \frac{s}{\sqrt{n}}$

for μ when σ is unknown provides a pretty good approximation.

Let’s summarize

* When the population is normal and/or the sample is large, a confidence interval for unknown population mean μ when σ is known is:

$¯ x \pm z * \frac{σ}{\sqrt{n}}$ , where z* is 1.645 for 90% confidence, 2 for 95% confidence, and 2.576 for 99% confidence.

* There is a trade-off between the level of confidence and the precision of the interval estimation. The price we have to pay for more precision is sacrificing level of confidence.

* The general form of confidence intervals is an estimate +/- the margin of error (m). In this case,the estimate= $¯ x$ and $m = z * \frac{σ}{\sqrt{n}}$ . The confidence interval is therefore centered at the estimate and its width is exactly 2m.

* For a given level of confidence, the width of the interval depends on the sample size. We can therefore do a sample size calculation to figure out what sample size is needed in order to get a confidence interval with a desired margin of error m, and a certain level of confidence (assuming we have some flexibility with the sample size). To do the sample size calculation we use:

$n = {(\frac{^{*} σ}{m})}^{2}$

(and round up to the next integer).

* When σ is unknown, we use the sample standard deviation, s, instead, but as a result we also need to use a different set of confidence multipliers (t*) associated with the t distribution. The interval is therefore

$¯ x \pm t^{*} * \frac{s}{\sqrt{n}}$

* These new multipliers have the added complexity that they depend not only on the level of confidence, but also on the sample size. Software is therefore very useful for calculating confidence intervals in this case.

* For large values of n, the t* multipliers are not that different from the z* multipliers, and therefore using the interval formula:

$¯ x \pm z^{*} * \frac{s}{\sqrt{n}}$

for μ when σ is unknown provides a pretty good approximation.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intro to Statistics MAT1260 by SBCCOE is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Overview

Comment

The General Case

Comment

Comment

Other Levels of Confidence

Understanding the general structure of the confidence intervals

Confidence Intervals for the Population Mean

Comment

Sample Size Calculations

Comment

When Is It Safe to Use the Confidence Interval We Developed?

Confidence Intervals for the Population Mean

Comments

Final comment

Let’s summarize

License

Share This Book