8.2: Hypothesis Tests for Proportions
Learning Objectives
- In a given context, specify the null and alternative hypotheses for the population proportion and mean.
- Carry out hypothesis testing for the population proportion and mean (when appropriate), and draw conclusions in context.
- Apply the concepts of: sample size, statistical significance vs. practical importance, and the relationship between hypothesis testing and confidence intervals.
Overview
Now that we understand the process we go through in hypothesis testing and the logic behind it, we are ready to start learning about specific statistical tests (also known as significance tests).
The first test we are going to learn is the test about the population proportion (p). This is test is widely known as the z-test for the population proportion (p). (We will understand later where the “z-test” part comes from.)
When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test.
Learn by Doing
Our discussion of hypothesis testing for the population proportion p follows the four steps of hypotheses testing that we introduced in our general discussion on hypothesis testing, but this time we go into more details. More specifically, we learn how the test statistic and p-value are calculated and interpreted.
Once we learn how to carry out the test for the population proportion p, we discuss some general topics that are related to hypotheses testing. More specifically, we see what role the sample size plays and understand how hypothesis testing and interval estimation (confidence intervals) are related.
Let’s start by introducing the three examples, which will be the leading examples in our discussion. Each example is followed by a figure illustrating the information provided, as well as the question of interest.
Example 1
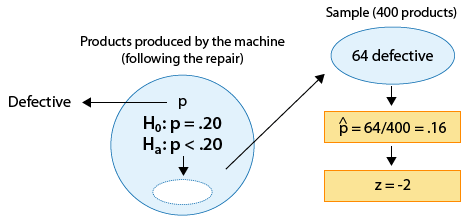
A machine is known to produce 20% defective products, and is therefore sent for repair. After the machine is repaired, 400 products produced by the machine are chosen at random and 64 of them are found to be defective. Do the data provide enough evidence that the proportion of defective products produced by the machine (p) has been reduced as a result of the repair?
The following figure displays the information, as well as the question of interest:

The question of interest helps us formulate the null and alternative hypotheses in terms of p, the proportion of defective products produced by the machine following the repair:
Ho: p = .20 (No change; the repair did not help).
Ha: p < .20 (The repair was effective).
Example 2
There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 100 students from the college, 19 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is .157? (This number is reported by the Harvard School of Public Health.)
Again, the following figure displays the information as well as the question of interest:

As before, we can formulate the null and alternative hypotheses in terms of p, the proportion of students in the college who use marijuana:
Ho: p = .157 (same as among all college students in the country).
Ha: p > .157 (higher than the national figure).
Example 3
Polls on certain topics are conducted routinely in order to monitor changes in the public’s opinions over time. One such topic is the death penalty. In 2003 a poll estimated that 64% of U.S. adults support the death penalty for a person convicted of murder. In a more recent poll, 675 out of 1,000 U.S. adults chosen at random were in favor of the death penalty for convicted murderers. Do the results of this poll provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers (p) changed between 2003 and the later poll?
Here is a figure that displays the information, as well as the question of interest:

Again, we can formulate the null and alternative hypotheses in term of p, the proportion of U.S. adults who support the death penalty for convicted murderers.
Ho: p =.64 (No change from 2003).
Ha: p ≠.64 (Some change since 2003).
Learn by Doing
According to the American Association of Community Colleges, 23% of community college students receive federal grants. The California Community College Chancellor’s Office anticipates that the percentage is smaller for California community college students. They collect a sample of 1,000 community college students in California and find that 210 received federal grants.
Did I get this?
Using data from 2008, the American Association of Community Colleges (AACC) reports that community college students constitute 46% of all U.S. undergraduates. Given the downturn in the U.S. economy, the AACC anticipates an increase in this percentage for 2010. A poll of 500 randomly chosen undergraduates taken in 2010 indicates that 52% are attending a community college.
Recall that there are basically 4 steps in the process of hypothesis testing:
1. State the null and alternative hypotheses.
2. Collect relevant data from a random sample and summarize them (using a test statistic).
3. Find the p-value, the probability of observing data like those observed assuming that Ho is true.
4. Based on the p-value, decide whether we have enough evidence to reject Ho (and accept Ha), and draw our conclusions in context.
We are now going to go through these steps as they apply to the hypothesis testing for the population proportion p. It should be noted that even though the details will be specific to this particular test, some of the ideas that we will add apply to hypothesis testing in general.
1. Stating the Hypotheses
Here again are the three set of hypotheses that are being tested in each of our three examples:
Example 1
Has the proportion of defective products been reduced as a result of the repair?
Ho: p = .20 (No change; the repair did not help).
Ha: p < .20 (The repair was effective).
Example 2
Is the proportion of marijuana users in the college higher than the national figure?
Ho: p = .157 (Same as among all college students in the country).
Ha: p > .157 (Higher than the national figure).
Example 3
Did the proportion of U.S. adults who support the death penalty changebetween 2003 and a later poll?
Ho: p =.64 (No change from 2003).
Ha: p ≠.64 (Some change since 2003).
Note that the null hypothesis always takes the form:
Ho: p = some value
and the alternative hypothesis takes one of the following three forms:
Ha: p < that value (like in example 1) or
Ha: p > that value (like in example 2) or
Ha: p ≠ that value (like in example 3).
Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value, and is generally denoted by po. We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form:
Ho: p = po
We write Ho: p = po to say that we are making the hypothesis that the population proportion has the value of po. In other words, p is the unknown population proportion and po is the number we think p might be for the given situation.
The alternative hypothesis takes one of the following three forms (depending on the context):
Ha: p < po(one-sided)
Ha: p > po(one-sided)
Ha: p ≠ po(two-sided)
The first two possible forms of the alternatives (where the = sign in Ho is challenged by < or >) are called one-sided alternatives, and the third form of alternative (where the = sign in Ho is challenged by ≠) is called atwo-sided alternative. To understand the intuition behind these names let’s go back to our examples.
Example 3 (death penalty) is a case where we have a two-sided alternative:
Ho: p =.64 (No change from 2003).
Ha: p ≠.64 (Some change since 2003).
In this case, in order to reject Ho and accept Ha we will need to get a sample proportion of death penalty supporters which is very different from .64 in either direction, either much larger or much smaller than .64.
In example 2 (marijuana use) we have a one-sided alternative:
Ho: p = .157 (Same as among all college students in the country).
Ha: p > .157 (Higher than the national figure).
Here, in order to reject Ho and accept Ha we will need to get a sample proportion of marijuana users which is much higher than .157.
Similarly, in example 1 (defective products), where we are testing:
Ho: p = .20 (No change; the repair did not help).
Ha: p < .20 (The repair was effective).
in order to reject Ho and accept Ha, we will need to get a sample proportion of defective products which is much smaller than .20.
Learn by Doing
In each of the following examples, a test for the population proportion (p) is called for. You are asked to select the right null and alternative hypotheses.
Scenario 1: The UCLA Internet Report (February 2003) estimated that roughly 8.7% of Internet users are extremely concerned about credit card fraud when buying online. Has that figure changed since? To test this, a random sample of 100 Internet users was chosen, and when interviewed, 10 said that they were extremely worried about credit card fraud when buying online. Let p be the proportion of all Internet users who are concerned about credit card fraud.
Scenario 2: The UCLA Internet Report (February 2003) estimated that a proportion of roughly .75 of online homes are still using dial-up access, but claimed that the use of dial-up is declining. Is that really the case? To examine this, a follow-up study was conducted a year later in which out of a random sample of 1,308 households that had Internet access, 804 were connecting using a dial-up modem. Let p be the proportion of all U.S. Internet-using households that have dial-up access.
Scenario 3: According to the UCLA Internet Report (February 2003) the use of the Internet at home is growing steadily and it is estimated that roughly 59.3% of households in the United States have Internet access at home. Has that trend continued since the report was released? To study this, a random sample of 1,200 households from a big metropolitan area was chosen for a more recent study, and it was found that 972 had an Internet connection. Let p be the proportion of U.S. households that have internet access.
Did I get this?
In each of the following examples, a test for the population proportion (p) is called for. You are asked to select the right null and alternative hypotheses.
Scenario 1: When shirts are made, there can occasionally be defects (such as improper stitching). But too many such defective shirts can be a sign of substandard manufacturing.
Suppose, in the past, your favorite department store has had only one defective shirt per 200 shirts (a prior defective rate of only .005). But you suspect that the store has recently switched to a substandard manufacturer. So you decide to test to see if their overall proportion of defective shirts today is higher.
Suppose that, in a random sample of 200 shirts from the store, you find that 27 of them are defective, for a sample proportion of defective shirts of .135. You want to test whether this is evidence that the store is “guilty” of substandard manufacturing, compared to their prior rate of defective shirts.
Scenario 2: It is a known medical fact that just slightly fewer females than males are born (although the reasons are not completely understood); the known “proper” baseline female birthrate is about 49% females.
In some cultures, male children are traditionally looked on more favorably than female children, and there is concern that the increasing availability of ultrasound may lead to pregnant mothers deciding to abort the fetus if it’s not the culturally “desired” gender. If this is happening, then the proportion of females in those nations would be significantly lower than the proper baseline rate.
To test whether the proportion of females born in India is lower than the proper baseline female birthrate, a study investigates a random sample of 6,500 births from hospital files in India, and finds 44.8% females born among the sample.
Scenario 3: A properly-balanced 6-sided game die should give a 1 in exactly 1/6 (16.7%) of all rolls. A casino wants to test its game die. If the die is not properly balanced one way or another, it could give either too many 1’s or too few 1’s, either of which could be bad.
The casino wants to use the proportion of 1’s to test whether the die is out of balance. So the casino test-rolls the die 60 times and gets a 1 in 9 of the rolls (15%).
2. Collecting and Summarizing the Data (Using a Test Statistic)
After the hypotheses have been stated, the next step is to obtain a sample (on which the inference will be based), collect relevant data, and summarize them.
It is extremely important that our sample is representative of the population about which we want to draw conclusions. This is ensured when the sample is chosen at random. Beyond the practical issue of ensuring representativeness, choosing a random sample has theoretical importance that we will mention later.
In the case of hypothesis testing for the population proportion (p), we will collect data on the relevant categorical variable from the individuals in the sample and start by calculating the sample proportion, [latex]\hat{p}[/latex] (the natural quantity to calculate when the parameter of interest is p).
Let’s go back to our three examples and add this step to our figures.
Example 1

Example 2

Example 3

As we mentioned earlier without going into details, when we summarize the data in hypothesis testing, we go a step beyond calculating the sample statistic and summarize the data with a test statistic. Every test has a test statistic, which to some degree captures the essence of the test. In fact, the p-value, which so far we have looked upon as “the king” (in the sense that everything is determined by it), is actually determined by (or derived from) the test statistic. We will now gradually introduce the test statistic.
The test statistic is a measure of how far the sample proportion [latex]\hat{p}[/latex] is from the null value p0, the value that the null hypothesis claims is the value of p. In other words, since [latex]\hat{p}[/latex] is what the data estimates p to be, the test statistic can be viewed as a measure of the “distance” between what the data tells us about p and what the null hypothesis claims p to be.
Let’s use our examples to understand this:
Example 1
The parameter of interest is p, the proportion of defective products following the repair.
The data estimate p to be [latex]\hat{p}=.16[/latex]
The null hypothesis claims that p = .20
The data are therefore .04 (or 4 percentage points) below the null hypothesis with respect to what they each tell us about p.
It is hard to evaluate whether this difference of 4% in defective products is enough evidence to say that the repair was effective, but clearly, the larger the difference, the more evidence it is against the null hypothesis. So if, for example, our sample proportion of defective products had been, say, .10 instead of .16, then I think you would all agree that cutting the proportion of defective products in half (from 20% to 10%) would be extremely strong evidence that the repair was effective.
Example 2
The parameter of interest is p, the proportion of students in a college who use marijuana.
The data estimate p to be [latex]\hat{p}=.19[/latex].
The null hypothesis claims that p = .157
The data are therefore .033 (or 3.3 percentage points) above the null hypothesis with respect to what they each tell us about p.
Example 3
The parameter of interest is p, the proportion of U.S. adults who support the death penalty for convicted murderers.
The data estimate p to be [latex]\hat{p}=.675[/latex]
The null hypothesis claims that p = .64.
There is a difference of .035 (3.5 percentage points) between the data and the null hypothesis with respect to what they each tell us about p.
There is a problem with just looking at the difference between the sample proportion [latex]\hat{p}[/latex] and the null value p0.
Examples 2 and 3 illustrate this problem very well.
In example 2 we have a difference of 3.3 percentage points between the data and the null hypothesis, which is approximately the same as the difference in example 3 of 3.5 percentage points. However, the difference in example 3 of 3.5 percentage points is based on a sample of size of 1,000 and therefore it is much more impressive than the difference of 3.3 percentage points in example 2, which was obtained from a sample of size of only 100.
Learn by Doing
For the reason illustrated in the examples at the end of the previous page, the test statistic cannot simply be the difference [latex]\hat{p}-p_{0}[/latex], but must be some form of that formula that accounts for the sample size. In other words, we need to somehow standardize the difference [latex]\hat{p}-p_{0}[/latex] so that comparison between different situations will be possible. We are very close to revealing the test statistic, but before we construct it, let’s be reminded of the following two facts from probability:
1. When we take a random sample of size n from a population with population proportion p, the possible values of the sample proportion [latex]\hat{p}[/latex] (when certain conditions are met) have approximately a normal distribution with:
* mean: p
standard deviation: [latex]\sqrt{\frac{\mathcal{p}\left(1-\mathcal{p}\right)}{\mathcal{n}}}[/latex]
2. The z-score of a normal value (a value that comes from a normal distribution) is:
[latex]\mathcal{z}=\frac{value-mean}{standard\ deviation}[/latex]
and it represents how many standard deviations below or above the mean the value is.
We are finally ready to reveal the test statistic:
The test statistic for this test measures the difference between the sample proportion [latex]\hat{p}[/latex] and the null value p0 by the z-score (standardized score) of the sample proportion [latex]\hat{p}[/latex], assuming that the null hypothesis is true (i.e., assuming that [latex]p-p_{0}[/latex]).
From fact 1, we know that the values of the sample proportion [latex]\hat{p}[/latex] are normal, and we are given the mean and standard deviation.
Using fact 2, we conclude that the z-score of [latex]\hat{p}[/latex] when [latex]\hat{p}-p_{0}[/latex] is:
[latex]\mathcal{z}=\frac{\hat{\mathcal{p}}-\mathcal{p}_0}{\sqrt{\frac{\mathcal{p}_0\left(1{-\mathcal{p}}_0\right)}{\mathcal{n}}}}[/latex]
This is the test statistic. It represents the difference between the sample proportion ([latex]\hat{p}[/latex]) and the null value ([latex]p_{0}[/latex]), measured in standard deviations.

Here is a representation of the sampling distribution of ˆp, assuming p = p0. In other words, this is a model of how ˆp‘s behave if we are drawing random samples from a population for which H0 is true. Notice the center of the sampling distribution is at p0, which is the hypothesized proportion given in the null hypothesis (H0: p = p0.) We could also mark the axis in standard deviation units, [latex]\sqrt{\frac{\mathcal{p}\left(1-\mathcal{p}\right)}{\mathcal{n}}}[/latex]. For example, if our null hypothesis claims that the proportion of U.S. adults supporting the death penalty is 0.64, then the sampling distribution is drawn as if the null is true. We draw a normal distribution centered at p = 0.64 with a standard deviation dependent on sample size, [latex]\sqrt{\frac{0.64(1-0.64)}{\mathcal{n}}}[/latex].
Important Comment
Note that under the assumption that H0 is true (i.e., [latex]p=p_{0}[/latex]), the test statistic, by the nature of the fact that it is a z-score, has N(0,1) (standard normal) distribution. Another way to say the same thing which is quite common is: “The null distribution of the test statistic is N(0,1).” By “null distribution,” we mean the distribution under the assumption that H0 is true. As we’ll see and stress again later, the null distribution of the test statistic is what the calculation of the p-value is based on.
Let’s go back to our three examples and find the test statistic in each case:
Example 1

Since the null hypothesis is H0: p = 0.20, the standardized score of ˆp=.16 is: [latex]\mathcal{z}=\frac{.16-.20}{\sqrt{\frac{.20\left(1-.20\right)}{400}}}=-2[/latex]
This is the value of the test statistic for this example.
What does this tell me?
This z-score of −2 tells me that (assuming that H0 is true) the sample proportion ˆp=.16 is 2 standard deviations below the null value (0.20).
Example 2
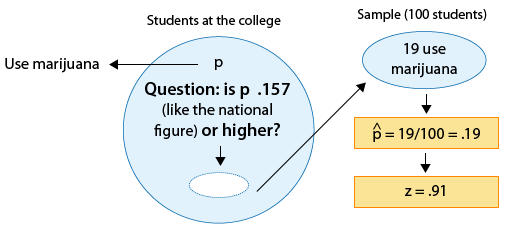
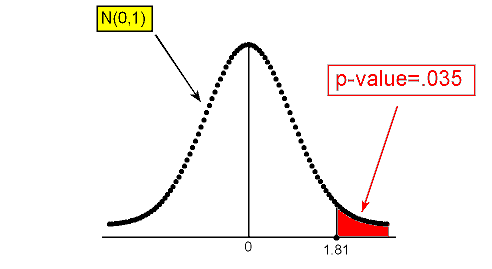
Since the null hypothesis is H0: p = 0.157, the standardized score of ˆp=.19 is: [latex]\mathcal{z}=\frac{.19-.157}{\sqrt{\frac{.157\left(1-.157\right)}{100}}}\approx.91[/latex].
This is the value of the test statistic for this example.
We interpret this to mean that, assuming that H0 is true, the sample proportion ˆp=.19 is 0.91 standard deviations above the null value (0.157).
Example 3

Since the null hypothesis is H0: p = 0.64, the standardized score of [latex]\hat{p}=.675[/latex] is: [latex]\mathcal{z}=\frac{.675-.64}{\sqrt{\frac{.64\left(1-.64\right)}{1000}}}\approx2.31[/latex].
This is the value of the test statistic for this example.
We interpret this to mean that, assuming that H0 is true, the sample proportion [latex]\hat{p}=.675[/latex] is 2.31 standard deviations above the null value (0.64).
Learn by Doing
We think that the most common color for automobiles is silver and that 24% of all automobiles sold are silver. We take a random sample of 225 cars and find that 63 of them are silver.
If we take a different random sample and get a test statistic of zero, what can we conclude? Mark each statement as true or false.
Comments about the Test Statistic
1. We mentioned earlier that to some degree, the test statistic captures the essence of the test. In this case, the test statistic measures the difference between ˆp and p0 in standard deviations. This is exactly what this test is about. Get data, and look at the discrepancy between what the data estimates p to be (represented by ˆp) and what H0 claims about p (represented by p0).
2. You can think about this test statistic as a measure of evidence in the data against H0. The larger the test statistic, the “further the data are from H0” and therefore the more evidence the data provide against H0.
Did I get this?
The UCLA Internet Report (February 2003) estimated that a proportion of roughly 0.75 of online homes are still using dial-up access, but claimed that the use of dial-up is declining. Is that really the case? To examine this, a follow-up study was conducted a year later in which, out of a random sample of 1,308 households that had Internet access, 804 were connecting using a dial-up modem.
Let p be the proportion of all U.S. Internet-using households who have dial-up access. In the previous activity, we established that the appropriate hypotheses here are:
H0: p = 0.75 and Ha: p < 0.75
Comments
-
-
It should now be clear why this test is commonly known as the z-test for the population proportion. The name comes from the fact that it is based on a test statistic that is a z-score.
-
Recall fact 1 that we used for constructing the z-test statistic. Here is part of it again:
When we take a random sample of size n from a population with population proportion p, the possible values of the sample proportion ([latex]\hat{p}[/latex]) (when certain conditions are met) have approximately a normal distribution with a mean of … and a standard deviation of ….
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:
-
The sample has to be random.
-
The conditions under which the sampling distribution of [latex]\hat{p}[/latex] is normal are met. In other words:

-
-
- Here we will pause to say more about condition (i.) above, the need for a random sample. In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population. We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them.
For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random. For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies. Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall.
Learn by Doing
We are conducting a survey to determine if an upcoming bond measure will receive a majority vote in the county. The null hypothesis claims that p = 0.50, where p is the proportion of registered voters in the county who say they support the bond measure.
Let’s check the conditions in our three examples.
Example 1
-
The 400 products were chosen at random.
-
n = 400, p0=.2, and therefore:

Example 2
-
The 100 students were chosen at random.
-
n = 100, p0=.157, and therefore:

Example 3
-
The 1,000 U.S. adults were chosen at random.
-
n = 1,000, p0=.64, and therefore:

Learn by Doing
In each of the following scenarios, you need to decide whether it is appropriate to use the z-test for the population proportion p, and if not, which condition is violated.
Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. So far we haven’t explicitly included it in the 4-step process of hypothesis testing, but now that we are discussing a specific test, you can see how it fits into the process. We are therefore now going to amend our 4-step process of hypothesis testing to include this extremely important part of the process.
The Four Steps in Hypothesis Testing
-
State the appropriate null and alternative hypotheses, Ho and Ha.
-
Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used. If the conditions are met, summarize the data using a test statistic.
-
Find the p-value of the test.
-
Based on the p-value, decide whether or not the results are significant and draw your conclusions in context.
With respect to the z-test, the population proportion that we are currently discussing:
Step 1: Completed
Step 2: Completed
Step 3: This is what we will work on next.
3. Finding the P-value of the Test
So far we’ve talked about the p-value at the intuitive level: understanding what it is (or what it measures) and how we use it to draw conclusions about the significance of our results. We will now go more deeply into how the p-value is calculated.
It should be mentioned that eventually we will rely on technology to calculate the p-value for us (as well as the test statistic), but in order to make intelligent use of the output, it is important to first understand the details, and only then let the computer do the calculations for us. Let’s start.
Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative) , the further [latex]\hat{p}[/latex] is from p0 , the more evidence we have against Ho. In the case of the p-value, it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho. One can actually draw conclusions in hypothesis testing just using the test statistic, and as we’ll see the p-value is, in a sense, just another way of looking at the test statistic. The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret. On the other hand, the p-value keeps its intuitive appeal across all statistical tests.
How is the p-value calculated?
Intuitively, the p-value is the probability of observing data like those observed assuming that Hois true. Let’s be a bit more formal:
-
Since this is a probability question about the data, it makes sense that the calculation will involve the data summary, the test statistic.
-
What do we mean by “like” those observed? By “like” we mean “as extreme or even more extreme.”
Putting it all together, we get that in general:
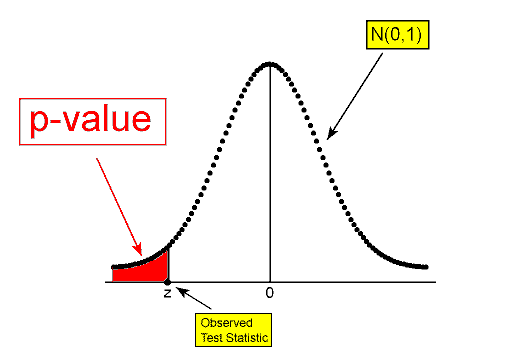
The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.
Comment
By “extreme” we mean extreme in the direction of the alternative hypothesis.
Specifically, for the z-test for the population proportion:
-
If the alternative hypothesis is Ha : p < p0 (less than), then “extreme” means small, and the p-value is:
The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
-
If the alternative hypothesis is Ha : p > p0 (greater than), then “extreme” means large, and the p-value is:
The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
-
if the alternative is [latex]H_{a}:p\neq p_{0}[/latex] (different from), then “extreme” means extreme in either direction either small or large (i.e., large in magnitude), and the p-value therefore is:
The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.
(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger.
If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)
OK, that makes sense. But how do we actually calculate it?
Recall the important comment from our discussion about our test statistic,
[latex]\mathcal{z}=\frac{\hat{\mathcal{p}}-\mathcal{p}_0}{\sqrt{\frac{\mathcal{p}_0\left(1{-\mathcal{p}}_0\right)}{\mathcal{n}}}}[/latex]
which said that when the null hypothesis is true (i.e., when p = p0 ), the possible values of our test statistic (because it is a z-score) follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.
Less Than
The probability of observing a test statistic as small as that observed or smaller, assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.
Greater Than
The probability of observing a test statistic as large as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution.
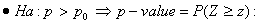

Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.
Not Equal To
The probability of observing a test statistic which is as large as in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.


This is often referred to as a two-tailed test, since we shaded in both directions.
As noted earlier, before the widespread use of statistical software, it was common to use ‘critical values’ instead of p-values to assess the evidence provided by the data. Even though the critical values approach is not used in this course, students might find it insightful. Thus, the interested students are encouraged to review the critical value method in the following “Many Students Wonder….” link. If your instructor clearly states that you are required to have knowledge of the critical value method, you should definitely review the information.
On the next page, we will apply the p-value to our three examples. But first, work through the following activities, which should help your understanding.
Learn by Doing
Let’s return to the scenario where we are studying the population of part-time college students. We know that in 2008, 60% of this population was female. We are curious if the proportion has decreased this year. We test the hypotheses: H0: p = 0.60 and Ha: p < 0.60, where p is the proportion of part-time college students that are female this year.
Did I get this?
In each of the following questions, choose the pair(s) of hypotheses for the population proportion (p) and the z statistic that match the figure.
Question 1:

Question 2:

Question 3:

Question 4:

Question 5:

Example 1
The p-value in this case is:
* The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.
OR (recalling what the test statistic actually means in this case),
* The probability of observing a sample proportion that is 2 standard deviations or more below p0 = .20, assuming that p0 is the true population proportion.
OR, more specifically,
* The probability of observing a sample proportion of .16 or lower in a random sample of size 400, when the true population proportion is p0 = .20.
In either case, the p-value is found as shown in the following figure:

To find [latex]P(Z\leq -2)[/latex] we can either use a table or software. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells me that it is pretty unlikely (probability of .023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.
Example 2
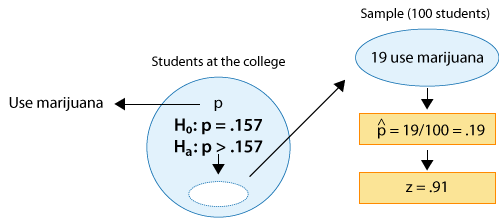
The p-value in this case is:
* The probability of observing a test statistic as large as .91 or larger, assuming that Ho is true.
OR (recalling what the test statistic actually means in this case),
* The probability of observing a sample proportion that is .91 standard deviations or more above p0 = .157, assuming that p0 is the true population proportion.
OR, more specifically,
* The probability of observing a sample proportion of .19 or higher in a random sample of size 100, when the true population proportion is p0 = .157.
In either case, the p-value is found as shown in the following figure:

Again, at this point we can either use a table or software to find that the p-value is 0.182.
The p-value tells us that it is not very surprising (probability of .182) to get data like those observed (which yield a test statistic of .91 or higher) assuming that the null hypothesis is true.
Example 3

The p-value in this case is:
* The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
OR (recalling what the test statistic actually means in this case),
* The probability of observing a sample proportion that is 2.31 standard deviations or more away from p0 = .64, assuming that p0 is the true population proportion.
OR, more specifically,
* The probability of observing a sample proportion as different as .675 is from .64, or even more different (i.e. as high as .675 or higher or as low as .605 or lower) in a random sample of size 1,000, when the true population proportion is p0 = .64.
In either case, the p-value is found as shown in the following figure:

Again, at this point we can either use a table or software to find that the p-value is 0.021.
The p-value tells us that it is pretty unlikely (probability of .021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.
Comment
We’ve just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.
Similarly, in any test, p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the “null distribution” of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1). As we’ll see, in other tests, other distributions come up (like the t-distribution and the F-distribution), which we will just mention briefly, and rely heavily on the output of our statistical package for obtaining the p-values.
We’ve just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion. Let’s go back to the four-step process of hypothesis testing and see what we’ve covered and what still needs to be discussed.
The Four Steps in Hypothesis Testing
-
State the appropriate null and alternative hypotheses, Ho and Ha.
-
Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used. If the conditions are met, summarize the data using a test statistic.
-
Find the p-value of the test.
-
Based on the p-value, decide whether or not the results are significant, and draw your conclusions in context.
With respect to the z-test the population proportion:
Step 1: Completed
Step 2: Completed
Step 3: Completed
Step 4: This is what we will work on next.
Learn by Doing
In 2007, a Gallup poll estimated that 45% of U.S. adults rated their financial situation as “good.” We want to know if the proportion is smaller this year. We gather a random sample of 100 U.S. adults this year and find that 39 rate their financial situation as “good.” Use the output from Minitab to complete the following statements about the p-value. Use numbers from the output to fill in the blanks.

Do zinc supplements reduce a child’s risk of catching a cold? A medical study reports a p-value of 0.03. Are the following interpretations of the p-value valid or invalid?
4. Drawing Conclusions Based on the p-Value
This last part of the four-step process of hypothesis testing is the same across all statistical tests, and actually, we’ve already said basically everything there is to say about it, but it can’t hurt to say it again.
The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.
We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.
It is important to mention again that this step has essentially two sub-steps:
-
Based on the p-value, determine whether or not the results are significant (i.e., the data present enough evidence to reject Ho).
-
State your conclusions in the context of the problem.
Let’s go back to our three examples and draw conclusions.
Example 1
(Has the proportion of defective products been reduced from 0.20 as a result of the repair?)
We found that the p-value for this test was 0.023.
Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho and conclude that as a result of the repair the proportion of defective products has been reduced to below 0.20. The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:

Example 2
(Is the proportion of students who use marijuana at the college higher than the national proportion, which is 0.157?)
We found that the p-value for this test was 0.182.
Since 0.182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.
We therefore do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure. Here is the complete story of this example:

Example 3
(Has the proportion of U.S. adults who support the death penalty for convicted murderers changed since 2003, when it was 0.64?)
We found that the p-value for this test was 0.021.
Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho, and we conclude that the proportion of adults who support the death penalty for convicted murderers has changed since 2003. Here is the complete story of this example:

Did I get this?
Two hypothesis tests were conducted.
In test I, a significance level of 0.05 was used, and the p-value was calculated to be 0.025.
In test II, a significance level of 0.01 was used, and the p-value was calculated to be 0.025.
Let’s Summarize
We have now completed going through the four steps of hypothesis testing, and in particular, we learned how they are applied to the z-test for the population proportion. Let’s briefly summarize:
Step 1
State the null and alternative hypotheses:
H0 : p = p0

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.
Step 2
Obtain data from a sample and:
(i) Check whether the data satisfy the conditions which allow you to use this test.
-
Random sample (or at least a sample that can be considered random in context)
-
n ⋅ p0 ≥ 10, n ⋅ (1 − p0) ≥ 10
(ii) Calculate the sample proportion [latex]\hat{p}[/latex], and summarize the data using the test statistic:
[latex]\mathcal{z}=\frac{\hat{\mathcal{p}}-\mathcal{p}_0}{\sqrt{\frac{\mathcal{p}_0\left(1{-\mathcal{p}}_0\right)}{\mathcal{n}}}}[/latex]
(Recall: This standardized test statistic represents how many standard deviations above or below po our sample proportion [latex]\hat{p}[/latex] is. )
Step 3
Find the p-value of the test either by using software or by using the test statistic as follows:
* for Ha:p<p0:P(Z≤z)
* for Ha:p>p0:P(Z≥z)
* for Ha:p≠p0:2P(Z≥|z|)
Step 4
Reach a conclusion first regarding the significance of the results, and then determine what it means in the context of the problem. Recall that:
If the p-value is small (in particular, smaller than the significance level, which is usually .05), the results are significant (in the sense that there is a significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho. If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Homay be true. (Remember, in hypothesis testing we never “accept” Ho).
More About Hypothesis Testing
The issues regarding hypothesis testing that we will discuss are:
1. The effect of sample size on hypothesis testing.
2. Statistical significance vs. practical importance. (This will be discussed in the activity following number 1.)
3. One-sided alternative vs. two-sided alternative—understanding what is going on.
4. Hypothesis testing and confidence intervals—how are they related?
Let’s start.
1. The Effect of Sample Size on Hypothesis Testing
We have already seen the effect that the sample size has on inference, when we discussed point and interval estimation for the population mean (μ) and population proportion (p). Intuitively…
Larger sample sizes give us more information to pin down the true nature of the population. We can therefore expect the sample mean and sample proportion obtained from a larger sample to be closer to the population mean and proportion, respectively. As a result, for the same level of confidence, we can report a smaller margin of error, and get a narrower confidence interval. What we’ve seen, then, is that larger sample size gives a boost to how much we trust our sample results. In hypothesis testing, larger sample sizes have a similar effect. The following two examples will illustrate that a larger sample size provides more convincing evidence, and how the evidence manifests itself in hypothesis testing. Let’s go back to our example 2 (marijuana use at a certain liberal arts college).
Example
2

The data do not provide enough evidence that the proportion of marijuana users at the college is higher than the proportion among all U.S. college students, which is .157. So far, nothing new. Let’s make small changes to the problem (and call it example 2*). The changes are highlighted and the problem is followed by a new figure that reflects the changes.
Example
2*
There are rumors that students in a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is .157? (reported by the Harvard School of Public Health).

We now have a larger sample (400 instead of 100), and also we changed the number of marijuana users (76 instead of 19).
Let’s carry out the test in this case.
I. The question of interest did not change, so we are testing the same hypotheses:
Ho: p = .157
Ha: p > .157
II. We select a random sample of size 400 and find that 76 are marijuana users.
(Note that the data satisfy the conditions that allow us to use this test. Verify this yourself).
Let’s summarize the data:

This is the same sample proportion as in the original problem, so it seems that the data give us the same evidence, but when we calculate the test statistic, we see that actually this is not the case:
![z = (.19 - .157) / √[( .157 (1 - .157) )/400 ] ≈ 1.81 z = (.19 - .157) / √[( .157 (1 - .157) )/400 ] ≈ 1.81](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u5_inference/_m1_inference_one_variable/webcontent/image290.gif)
Even though the sample proportion is the same (.19), since here it is based on a larger sample (400 instead of 100), it is 1.81 standard deviations above the null value of .157 (as opposed to .91 standard deviations in the original problem).
III. For the p-value, we use statistical software to find p-value = 0.035.
The p-value here is .035 (as opposed to .182 in the original problem). In other words, when Ho is true (i.e. when p=.157) it is quite unlikely (probability of .035) to get a sample proportion of .19 or higher based on a sample of size 400 (probability .035), and not very unlikely when the sample size is 100 (probability .182).
IV.
Our results here are significant. In other words, in example 2* the data provide enough evidence to reject Ho and conclude that the proportion of marijuana users at the college is higher than among all U.S. students.
Let’s summarize with a figure:

What do we learn from these two examples?
We see that sample results that are based on a larger sample carry more weight.
In example 2, we saw that a sample proportion of .19 based on a sample of size of 100 was not enough evidence that the proportion of marijuana users in the college is higher than .157. Recall, from our general overview of hypothesis testing, that this conclusion (not having enough evidence to reject the null hypothesis) doesn’t mean the null hypothesis is necessarily true (so, we never “accept” the null); it only means that the particular study didn’t yield sufficient evidence to reject the null. It might be that the sample size was simply too small to detect a statistically significant difference.
However, in example 2*, we saw that when the sample proportion of .19 is obtained from a sample of size 400, it carries much more weight, and in particular, provides enough evidence that the proportion of marijuana users in the college is higher than .157 (the national figure). In this case, the sample size of 400 was large enough to detect a statistically significant difference.
The following activity will allow you to practice the ideas and terminology used in hypothesis testing when a result is not statistically significant.
Learn by Doing
Suppose that only 40% of the U.S. public supported the general direction of the previous U.S. administration’s policies. To gauge whether the nationwide proportion, p, of support for the current administration is higher than 40%, a major polling organization conducts a random poll to test the hypotheses:
Ho: p = .40
Ha: p > .40
The results are reported to be not statistically significant, with ap-value of .214.
Decide whether each of the following statements is a valid conclusion or an invalid conclusion, based on the study:
3. One-Sided Alternative vs. Two-Sided Alternative
Recall that earlier we noticed (only visually) that for a given value of the test statistic z, the p-value of the two-sided test is twice as large as the p-value of the one-sided test. We will now further discuss this issue. In particular, we will use our example 2 (marijuana users at a certain college) to gain better intuition about this fact.
For illustration purposes, we are actually going to use example 2* (where out of a sample of size 400, 76 were marijuana users). Let’s recall example 2*, but this time give two versions of it; the original version, and a slightly changed version, which we’ll call example 2**. The differences are highlighted.
Example
2*
There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is .157? (This number is reported by the Harvard School of Public Health.)
Example
2**
The dean of students in a certain liberal arts college was interested in whether the proportion of students who use drugs in her college is different than the proportion among U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) differs from the national proportion, which is .157? (This number is reported by the Harvard School of Public Health.)
Learn by Doing
Indeed, in example 2* we suspect from the outset (based on the rumors) that the overall proportion (p) of marijuana smokers at the college is higher than the reported national proportion of .157, and therefore the appropriate alternative is Ho:p>.157. In example 2**, as a result of the change of wording (which eliminated the part about the rumors), we simply wonder if p is different (in either direction) from the reported national proportion of .157, and therefore the appropriate alternative is the two-sided test: Ha:p≠p0. Would switching to the two-sided alternative have an effect on our results?
Let’s explore that.
Example
2*
We already carried out the test for this example, and the results are summarized in the following figure:

The following figure reminds you how the p-value was found (using the test statistic):
Example
2**
I. Here we are testing:

II. Since we have the same data as in example 2* (76 marijuana users out of 400), we have the same sample proportion and the same test statistic:
III. Since the calculation of the p-value depends on the type of alternative we have, here is where things start to be different. Statistical software tells us that the p-value for example 2** is 0.070. Here is a figure that reminds us how the p-value was calculated (based on the test statistic):

IV. If we use the .05 level of significance, the p-value we got is not small enough (.07>.05), and therefore we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the proportion of marijuana smokers in the college is different from the national proportion (.157).
What happened here?
It should be pretty clear what happened here numerically. The p-value of the one-sided test (example 2*) is .035, suggesting the results are significant at the .05 significant level. However, the p-value of the two sided-test (example 2**) is twice the p-value of the one-sided test, and is therefore 2*.035=.07, suggesting that the results are not significant at the .05 significance level.
Here is a more conceptual explanation:
The idea is that in Example 2*, we began our hypothesis test with a piece of information (in the form of a rumor) about unknown population proportion p, which gave us a sort of head-start towards the goal of rejecting the null hypothesis. We foundthat the evidence that the data provided were then enough to cross the finish line and reject Ho. In Example 2**, we had no prior information to go on, and the data alone were not enough evidence to cross the finish line and reject Ho. The following figure illustrates this idea:

We can summarize and say that in general it is harder to reject Ho against a two-sided Ha because the p-value is twice as large. Intuitively, a one-sided alternative gives us a head-start, and on top of that we have the evidence provided by the data. When our alternative is the two-sided test, we get no head-start and all we have are the data, and therefore it is harder to cross the finish line and reject Ho.
Did I get this?
Consider the following two hypothesis testing scenarios for the population proportion (p) and corresponding studies:
I. The UCLA Internet Report (February 2003) estimated that roughly 8.7% of Internet users are extremely concerned about credit card fraud when buying online. A study was designed in order to examine whether that proportion has changed since.
II.The UCLA Internet Report (February 2003) estimated that roughly 8.7% of Internet users are extremely concerned about credit card fraud when buying online. In light of the increasing problem of spyware, a study was designed in order to examine whether that proportion has increased since.
4. Hypothesis Testing and Confidence Intervals
The last topic we want to discuss is the relationship between hypothesis testing and confidence intervals. Even though the flavor of these two forms of inference is different (confidence intervals estimate a parameter, and hypothesis testing assesses the evidence in the data against one claim and in favor of another), there is a strong link between them.
We will explain this link (using the z-test and confidence interval for the population proportion), and then explain how confidence intervals can be used after a test has been carried out.
Recall that a confidence interval gives us a set of plausible values for the unknown population parameter. We may therefore examine a confidence interval to informally decide if a proposed value of population proportion seems plausible.
For example, if a 95% confidence interval for p, the proportion of all U.S. adults already familiar with Viagra in May 1998, was (.61, .67), then it seems clear that we should be able to reject a claim that only 50% of all U.S. adults were familiar with the drug, since based on the confidence interval, .50 is not one of the plausible values for p.
In fact, the information provided by a confidence interval can be formally related to the information provided by a hypothesis test. (Comment: The relationship is more straightforward for two-sided alternatives, and so we will not present results for the one-sided cases.)
Suppose we want to carry out the two-sided test:

using a significance level of .05.
An alternative way to perform this test is to find a 95% confidence interval for p and check:
If p0 falls outside the confidence interval, reject Ho.
If p0 falls inside the confidence interval, do not reject Ho.
In other words, if p0 is not one of the plausible values for p, we reject Ho.
If p0 is a plausible value for p, we cannot reject Ho.
(Comment: Similarly, the results of a test using a significance level of .01 can be related to the 99% confidence interval.)
Let’s look at two examples:
Example
Recall example 3, where we wanted to know whether the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was .64.

We are testing:

and as the figure reminds us, we took a sample of 1,000 U.S. adults, and the data told us that 675 supported the death penalty for convicted murderers (i.e. [latex]\hat{p}=.675[/latex]).
A 95% confidence interval for p, the proportion of all U.S. adults who support the death penalty, is:
[latex].675\pm2\sqrt{\frac{.675(1-.675)}{1000}}\approx.675\pm.03=\left(.645,\ .705\right)[/latex]
Since the 95% confidence interval for p does not include .64 as a plausible value for p, we can reject Ho and conclude (as we did before) that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003.

Example
You and your roommate are arguing about whose turn it is to clean the apartment. Your roommate suggests that you settle this by tossing a coin and takes one out of a locked box he has on the shelf. Suspecting that the coin might not be fair, you decide to test it first. You toss the coin 80 times, thinking to yourself that if, indeed, the coin is fair, you should get around 40 heads. Instead you get 48 heads. You are puzzled. You are not sure whether getting 48 heads out of 80 is enough evidence to conclude that the coin is unbalanced, or whether this a result that could have happened just by chance when the coin is fair.
Statistics can help you answer this question.
Let p be the true proportion (probability) of heads. We want to test whether the coin is fair or not:

The data we have are that out of n=80 tosses, we got 48 heads, or that the sample proportion of heads is:[latex]\hat{p}=\frac{48}{80}=.6[/latex]
The 95% confidence interval for p, the true proportion of heads for this coin, is:
[latex].6\pm 2 \sqrt{\frac{.6(1-.6)}{80}}\approx .6\pm .11=(.49,.71)[/latex]
Since in this case .5 is one of the plausible values for p, we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the coin is not fair.

Did I get this?
The UCLA Internet Report (February 2003) estimated that roughly 8.7% of Internet users are extremely concerned about credit card fraud when buying online. A study was designed in order to examine whether that proportion has changed since. Let p be the proportion of all Internet users who are concerned about credit card fraud. In this study we are therefore testing:

Based on the collected data, a 95% confidence interval for p was found to be (.08, .14).
The UCLA Internet Report (February 2003) estimated that roughly 60.5% of U.S. adults use the Internet at work for personal use. A follow-up study was conducted in order to explore whether that figure has changed since. Let p be the proportion of U.S. adults who use the Internet at work for personal use.
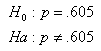
Based on the collected data, the p-value of the test was found to be .001.
Comment
The context of the last example is a good opportunity to bring up an important point that was discussed earlier.
Even though we use .05 as a cutoff to guide our decision about whether the results are significant, we should not treat it as inviolable and we should always add our own judgment. Let’s look at the last example again.
It turns out that the p-value of this test is .0734. In other words, it is maybe not extremely unlikely, but it is quite unlikely (probability of .0734) that when you toss a fair coin 80 times you’ll get a sample proportion of heads of 48/80=.6 (or even more extreme). It is true that using the .05 significance level (cutoff), .0734 is not considered small enough to conclude that the coin is not fair. However, if you really don’t want to clean the apartment, the p-value might be small enough for you to ask your roommate to use a different coin, or to provide one yourself!
Here is our final point on this subject:
When the data provide enough evidence to reject Ho, we can conclude (depending on the alternative hypothesis) that the population proportion is either less than, greater than or not equal to the null value [latex]p_{0}[/latex]. However, we do not get a more informative statement about its actual value. It might be of interest, then, to follow the test with a 95% confidence interval that will give us more insight into the actual value of p.
Example
In our example 3,

we concluded that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was .64. It is probably of interest not only to know that the proportion has changed, but also to estimate what it has changed to. We’ve calculated the 95% confidence interval for p on the previous page and found that it is (.645, .705).
We can combine our conclusions from the test and the confidence interval and say:
Data provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, and we are 95% confident that it is now between .645 and .705. (i.e. between 64.5% and 70.5%).
Example
Let’s look at our example 1 to see how a confidence interval following a test might be insightful in a different way.
Here is a summary of example 1:

We conclude that as a result of the repair, the proportion of defective products has been reduced to below .20 (which was the proportion prior to the repair). It is probably of great interest to the company not only to know that the proportion of defective has been reduced, but also estimate what it has been reduced to, to get a better sense of how effective the repair was. A 95% confidence interval for p in this case is:
[latex].16\pm2\sqrt{\frac{.16(1-.16)}{400}}\approx.16\pm.037=\left(.129,\ .197\right)[/latex]
We can therefore say that the data provide evidence that the proportion of defective products has been reduced, and we are 95% sure that it has been reduced to somewhere between 12.9% and 19.7%. This is very useful information, since it tells us that even though the results were significant (i.e., the repair reduced the number of defective products), the repair might not have been effective enough, if it managed to reduce the number of defective products only to the range provided by the confidence interval. This, of course, ties back in to the idea of statistical significance vs. practical importance that we discussed earlier. Even though the results are significant (Ho was rejected), practically speaking, the repair might be considered ineffective.
Let’s summarize
Even though this unit is about the z-test for population proportion, it is loaded with very important ideas that apply to hypothesis testing in general. We’ve already summarized the details that are specific to the z-test for proportions, so the purpose of this summary is to highlight the general ideas.
The process of hypothesis testing has four steps:
I. Stating the null and alternative hypotheses (Ho and Ha).
II. Obtaining a random sample (or at least one that can be considered random) and collecting data. Using the data:
* Check that the conditions under which the test can be reliably used are met.
* Summarize the data using a test statistic.
The test statistic is a measure of the evidence in the data against Ho. The larger the test statistic is in magnitude, the more evidence the data present against Ho.
III. Finding the p-value of the test.
The p-value is the probability of getting data like those observed (or even more extreme) assuming that the null hypothesis is true, and is calculated using the null distribution of the test statistic. The p-value is a measure of the evidence against Ho. The smaller the p-value, the more evidence the data present against Ha.
IV. Making conclusions.
– Conclusions about the significance of the results:
If the p-value is small, the data present enough evidence to reject Ho (and accept Ha).
If the p-value is not small, the data do not provide enough evidence to reject Ho.
To help guide our decision, we use the significance level as a cutoff for what is considered a small p-value. The significance cutoff is usually set at .05, but should not be considered inviolable.
– Conclusions in the context of the problem.
Results that are based on a larger sample carry more weight, and therefore as the sample size increases, results become more significant.
Even a very small and practically unimportant effect becomes statistically significant with a large enough sample size. The distinction between statistical significance and practical importance should therefore always be considered.
For given data, the p-value of the two-sided test is always twice as large as the p-value of the one-sided test. It is therefore harder to reject Ho in the two-sided case than it is in the one-sided case in the sense that stronger evidence is required. Intuitively, the hunch or information that leads us to use the one-sided test can be regarded as a head-start toward the goal of rejecting Ho.
Confidence intervals can be used in order to carry out two-sided tests (at the .05 significance level). If the null value is not included in the confidence interval (i.e., is not one of the plausible values for the parameter), we have enough evidence to reject Ho. Otherwise, we cannot reject Ho.
If the results are significant, it might be of interest to follow up the tests with a confidence interval in order to get insight into the actual value of the parameter of interest.

