5.4: Binomial Distribution
Binomial Random Variables
So far, in our discussion about discrete random variables, we have been introduced to:
-
The probability distribution, which tells us which values a variable takes, and how often it takes them.
-
The mean of the random variable, which tells us the long-run average value that the random variable takes.
-
The standard deviation of the random variable, which tells us a typical (or long-run average) distance between the mean of the random variable and the values it takes.
We now introduce a special class of discrete random variables that are very common because, as you’ll see, they come up in many situations: binomial random variables.
Here’s how we’ll present this material. First, we’ll explain what kind of random experiments give rise to a binomial random variable and how the binomial random variable is defined in those types of experiments.
We’ll then present the probability distribution of the binomial random variable, which will be presented as a formula (which, as you remember, is one of the three ways in which a probability distribution of a discrete random variable can be presented), and explain why the formula makes sense. We’ll conclude our discussion by presenting the mean and standard deviation of the binomial random variable.
As we just mentioned, we’ll start by describing what kind of random experiments give rise to a binomial random variable. We’ll call this type of random experiment a “binomial experiment.”
Binomial Experiment
Binomial experiments are random experiments that consist of a fixed number of repeated trials, like tossing a coin 10 times, randomly choosing 10 people, rolling a die 5 times, etc. These trials, however, need to be independent in the sense that the outcome in one trial has no effect on the outcome in other trials. In each of these repeated trials there is one outcome that is of interest to us (we call this outcome “success”), and each of the trials is identical in the sense that the probability that the trial will end in a “success” is the same in each of the trials. So for example, if our experiment is tossing a coin 10 times, and we are interested in the outcome “heads” (our “success”), then this will be a binomial experiment, since the 10 trials are independent, and the probability of success is 1/2 in each of the 10 trials. Let’s summarize and give more examples.
To summarize, the requirements for a random experiment to be a binomial experiment are as follows:
- A fixed number (n) of trials
- Each trial must be independent of the others
- Each trial has just two possible outcomes, called success (the outcome of interest) and failure
- There is a constant probability (p) of success for each trial, the complement of which is the probability (1 – p) of failure
In binomial random experiments, the number of successes in n trials is random. It can be as low as 0, if all the trials end up in failure, or as high as n, if all n trials end in success.
The random variable X that represents the number of successes in those n trials is called binomial, and is determined by the values of n and p. We say, “X is binomial with n = … and p = …”
Example
Random Experiments (Binomial or Not?)
Let’s consider a few random experiments.
In each of them, we’ll decide whether the random variable is binomial. If it is, we’ll determine the values for n and p. If it isn’t, we’ll explain why not.
-
A fair coin is flipped 20 times; X represents the number of heads.
X is binomial with n = 20 and p = 0.5.
-
You roll a fair die 50 times; X is the number of times you get a six.
X is binomial with n = 50 and p = 1/6.
-
Roll a fair die repeatedly; X is the number of rolls it takes to get a six.
X is not binomial, because the number of trials is not fixed.
-
Draw 3 cards at random, one after the other, without replacement, from a set of 4 cards consisting of one club, one diamond, one heart, and one spade; X is the number of diamonds selected.
X is not binomial, because the selections are not independent. (The probability (p) of success is not constant, because it is affected by previous selections.)
-
Draw 3 cards at random, one after the other, with replacement, from a set of 4 cards consisting of one club, one diamond, one heart, and one spade; X is the number of diamonds selected. Sampling with replacement ensures independence.
X is binomial with n = 3 and p = 1/4.
-
Approximately 1 in every 20 children has a certain disease. Let X be the number of children with the disease out of a random sample of 100 children. Although the children are sampled without replacement, it is assumed that we are sampling from such a vast population that the selections are virtually independent.
X is binomial with n = 100 and p = 1/20 = 0.05.
-
The probability of having blood type B is 0.1. Choose 4 people at random; X is the number with blood type B.
X is binomial with n = 4 and p = 0.1.
-
A student answers 10 quiz questions completely at random; the first five are true/false, the second five are multiple choice, with four options each. X represents the number of correct answers.
X is not binomial, because p changes from 1/2 to 1/4.
Comments
Example D above was not binomial because sampling without replacement resulted in dependent selections. In particular, the probability of the second card being a diamond is very dependent on whether or not the first card was a diamond: the probability is 0 if the first card was a diamond, 1/3 if the first card was not a diamond.
In contrast, Example E was binomial because sampling with replacement resulted in independent selections: the probability of any of the 3 cards being a diamond is 1/4 no matter what the previous selections have been.
On the other hand, when you take a relatively small random sample of subjects from a large population, even though the sampling is without replacement, we can assume independence because the mathematical effect of removing one individual from a very large population on the next selection is negligible. For example, in Example F, we sampled 100 children out of the population of all children. Even though we sampled the children without replacement, whether one child has the disease or not really has no effect on whether another child has the disease or not. The same is true for Example G.
The convention is to “fudge” the requirement of independence as long as the population is at least 10 times the sample size.
Rule of Thumb |
|---|
|
The number (X) of successes in a sample of size n taken without replacement from a population with proportion (p) of successes is approximately binomial with n and p as long as the sample size (n) is at most 10% of the population size (N). In symbols, this would be: n ≤ .10N. This is the same as saying the population size is greater than or equal to 10 times the sample size. In symbols this is: N ≥ 10n. |
Learn by Doing
A Department of Transportation report about air travel found that, nationwide, 78% of all flights are on time. Suppose a random sample of 50 flights is selected from all nationwide flights that were completed in the past 30 days (over 1000 flights). Let the random variable X be defined as the number of sampled flights that arrived on time.
Did I get this?
Did I get this?
Now that we understand what a binomial random variable is, and when it arises, it’s time to discuss its probability distribution. We’ll start with a simple example and then generalize to a formula.
Example
Deck of Cards
Consider a regular deck of 52 cards, in which there are 13 cards of each suit: hearts, diamonds, clubs and spades. We select 3 cards at random with replacement. Let X be the number of diamond cards we got (out of the 3).
We have 3 trials here, and they are independent (since the selection is with replacement). The outcome of each trial can be either success (diamond) or failure (not diamond), and the probability of success is 1/4 in each of the trials.
X, then, is binomial with n = 3 and p = 1/4.
Let’s build the probability distribution of X as we did in the chapter on probability distributions. Recall that we begin with a table in which we:
-
record all possible outcomes in 3 selections, where each selection may result in success (a diamond, D) or failure (a non-diamond, N).
-
find the value of X that corresponds to each outcome.
-
use simple probability principles to find the probability of each outcome.
![A table of all of the outcomes. Here is the data in the table, given in "Outcome: Value of X, Probability" format: NNN: 0, 3/4 × 3/4 × 3/4; NND: 1, 3/4 × 3/4 × 1/4; NDN: 1, 3/4 × 1/4 × 3/4; DNN: 1, 1/4 × 3/4 × 3/4; NDD: 2, 3/4 × 1/4 × 1/4; DND: 2, 1/4 × 3/4 × 1/4; DDN: 2, 1/4 × 1/4 × 1/4; DDD: 3, 1/4 × 1/4 × 1/4;](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image078.gif "A table of all of the outcomes. Here is the data in the table, given in "Outcome: Value of X, Probability" format: NNN: 0, 3/4 × 3/4 × 3/4; NND: 1, 3/4 × 3/4 × 1/4; NDN: 1, 3/4 × 1/4 × 3/4; DNN: 1, 1/4 × 3/4 × 3/4; NDD: 2, 3/4 × 1/4 × 1/4; DND: 2, 1/4 × 3/4 × 1/4; DDN: 2, 1/4 × 1/4 × 1/4; DDD: 3, 1/4 × 1/4 × 1/4;")
With the help of the addition principle, we condense the information in this table to construct the actual probability distribution table:
![The probability distribution table has two rows, labeled "X" and "P(X=x)." Here is the data in the table, organized by column. The format is "(X, P(X=x))" 0: 1(3/4)³ 1: 3(1/4)¹(3/4)² 2: 3(1/4)²(3/4)¹ 3: 1(1/4)³](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image079.gif "The probability distribution table has two rows, labeled "X" and "P(X=x)." Here is the data in the table, organized by column. The format is "(X, P(X=x))" 0: 1(3/4)³ 1: 3(1/4)¹(3/4)² 2: 3(1/4)²(3/4)¹ 3: 1(1/4)³")
In order to establish a general formula for the probability that a binomial random variable X takes any given value x, we will look for patterns in the above distribution. From the way we constructed this probability distribution, we know that, in general:
![P(X=x) = [ Number of possible outcomes with x successes out of 3 ] × [ Probability that each of the outcomes that has x successes out of 3 ]](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image080.gif "P(X=x) = [ Number of possible outcomes with x successes out of 3 ] × [ Probability that each of the outcomes that has x successes out of 3 ]")
Let’s start with the second part, the probability that there will be x successes out of 3, where the probability of success is 1/4. Notice that the fractions multiplied in each case are for the probability of x successes (where each success has a probability of p = 1/4) and the remaining (3 – x) failures (where each failure has probability of 1 – p = 3/4).
![This probability distribution table is nearly the same as the previous one, but presents the calculations in a different way. The table has two rows, labeled "X" and "P(X=x)." Here is the data in the table, organized by column. The format is "(X, P(X=x))" 0: 1 × (1/4)^0 × (3/4)^(3-0); 1: 3 × (1/4)^1 × (3/4)^(3-1); 2: 3 × (1/4)^2 × (3/4)^(3-2); 3: 1 × (1/4)^3 × (3/4)^(3-3);](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image081.gif "This probability distribution table is nearly the same as the previous one, but presents the calculations in a different way. The table has two rows, labeled "X" and "P(X=x)." Here is the data in the table, organized by column. The format is "(X, P(X=x))" 0: 1 × (1/4)^0 × (3/4)^(3-0); 1: 3 × (1/4)^1 × (3/4)^(3-1); 2: 3 × (1/4)^2 × (3/4)^(3-2); 3: 1 × (1/4)^3 × (3/4)^(3-3);")
So in general:
![[ Probability of each of the outcomes that has x successes out of 3 ] = (1/4)^x × (3/4)^(3-x)](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image082.gif "[ Probability of each of the outcomes that has x successes out of 3 ] = (1/4)^x × (3/4)^(3-x)")
Let’s move on to talk about the number of possible outcomes with x successes out of three. Here it is harder to see the pattern, so we’ll give the following mathematical result.
Result
Consider a random experiment that consists of n trials, each one ending up in either success or failure. The number of possible outcomes in the sample space that have exactly k successes out of n is:
[latex]\frac{\mathcal{n}!}{\mathcal{k}!\left(\mathcal{n}-\mathcal{k}\right)!}[/latex]
Note that n! is read “n factorial” and is defined to be the product 1 * 2 * 3 * … * n. 0! is defined to be 1.
Example
Ear Piercings
You choose 12 male college students at random and record whether they have any ear piercings (success) or not. There are many possible outcomes to this experiment (actually, 4,096 of them!).
In how many of the possible outcomes of this experiment are there exactly 8 successes (students who have at least one ear pierced)?
There is no way that we would start listing all these possible outcomes. The result above comes to our rescue.
The result says that in an experiment like this, where you repeat a trial n times (in our case, we repeat it n = 12 times, once for each student we choose), the number of possible outcomes with exactly 8 successes (out of 12) is:
[latex]\frac{12!}{8!\left(12-8\right)!}=\frac{1\times2\times3\times...\times12}{\left(1\times2\times3\times...\times8\right)\left(1\times2\times3\times4\right)}=495[/latex]
Did I get this?
Example
Cards Revisited
Let’s go back to our example, in which we have n = 3 trials (selecting 3 cards). We saw that there were 3 possible outcomes with exactly 2 successes out of 3. The result confirms this since:
[latex]\frac{3!}{2!\left(3-2\right)!}=\frac{1\times2\times3}{\left(1\times2\right)\left(1\right)}=3[/latex]
In general, then
![[ Number of possible outcomes with x successes out of 3 ] = ( 3! ) / [ x! × (3-x)! ]](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image086.gif "[ Number of possible outcomes with x successes out of 3 ] = ( 3! ) / [ x! × (3-x)! ]")
Putting it all together, we get that the probability distribution of X, which is binomial with n = 3 and p = 1/4 is:
[latex]\mathcal{P}\left(\mathcal{X}=\mathcal{x}\right)=\frac{3!}{\mathcal{x}!\left(3-\mathcal{x}\right)!}\left(\frac{1}{4}\right)^\mathcal{x}\left(\frac{3}{4}\right)^{3-\mathcal{x}}[/latex] for x= 0,1,2,3
In general, the number of ways to get x successes (and n – x failures) in n trials is [latex]\frac{\mathcal{n}!}{\mathcal{x}!\left(\mathcal{n}-\mathcal{x}\right)!}[/latex]
Therefore, the probability of x successes (and n – x failures) in n trials, where the probability of success in each trial is p (and the probability of failure is 1 – p) is equal to the number of outcomes in which there are x successes out of n trials, times the probability of x successes, times the probability of n – x failures:
[latex]\mathcal{P}\left(\mathcal{X}=\mathcal{x}\right)=\frac{\mathcal{n}!}{\mathcal{x}!\left(\mathcal{n}-\mathcal{x}\right)!}\left(\mathcal{p}\right)^\mathcal{x}\left(1-\mathcal{P}\right)^{\left(\mathcal{n}-\mathcal{x}\right)}[/latex]
where x may take any value 0, 1, … , n.
Let’s look at another example:
Example
Blood Type A
The probability of having blood type A is .4. Choose 4 people at random and let X be the number with blood type A.
X is a binomial random variable with n = 4 and p = .4.
As a review, let’s first find the probability distribution of X the long way: construct an interim table of all possible outcomes in S, the corresponding values of X, and probabilities. Then construct the probability distribution table for X.
![The probability distribution table, with three columns, "S," "X," and "Probability." Here is the data in the table, given in row format (S: X, Probability): NNNN: 0, .4^0 × .6^4; NNNA: 1, .4^1 × .6^3; NNAN: 1, .4^1 × .6^3; NANN: 1, .4^1 × .6^3; ANNN: 1, .4^1 × .6^3; NNAA: 2, .4^2 × .6^2; NANA: 2, .4^2 × .6^2; NAAN: 2, .4^2 × .6^2; ANNA: 2, .4^2 × .6^2; ANAN: 2, .4^2 × .6^2; AANN: 2, .4^2 × .6^2; NAAA: 3, .4^3 × .6^1; ANAA: 3, .4^3 × .6^1; AANA: 3, .4^3 × .6^1; AAAN: 3, .4^3 × .6^1; AAAA: 4, .4^4 × .6^0;](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image090.gif "The probability distribution table, with three columns, "S," "X," and "Probability." Here is the data in the table, given in row format (S: X, Probability): NNNN: 0, .4^0 × .6^4; NNNA: 1, .4^1 × .6^3; NNAN: 1, .4^1 × .6^3; NANN: 1, .4^1 × .6^3; ANNN: 1, .4^1 × .6^3; NNAA: 2, .4^2 × .6^2; NANA: 2, .4^2 × .6^2; NAAN: 2, .4^2 × .6^2; ANNA: 2, .4^2 × .6^2; ANAN: 2, .4^2 × .6^2; AANN: 2, .4^2 × .6^2; NAAA: 3, .4^3 × .6^1; ANAA: 3, .4^3 × .6^1; AANA: 3, .4^3 × .6^1; AAAN: 3, .4^3 × .6^1; AAAA: 4, .4^4 × .6^0;")
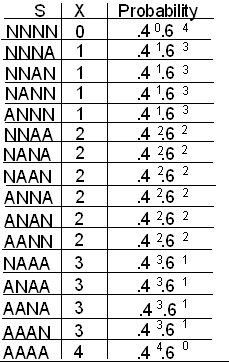
As usual, the addition rule lets us combine probabilities for each possible value of X:
![A table with two columns, labeled "X," and "Probability." Here is the data, in row format (X, Probability): 0: (1) × .4^0 × .6^4 = .1296; 1: (4) × .4^1 × .6^3 = .3456; 2: (6) × .4^2 × .6^2 = .3456; 3: (4) × .4^3 × .6^1 = .1536; 4: (1) × .4^4 × .6^0 = .0256;](https://oli.cmu.edu/repository/webcontent/72712ec00a0001dc418a87e73e8ebb77/_u4_probability/_m3_random_variables/webcontent/image091.gif "A table with two columns, labeled "X," and "Probability." Here is the data, in row format (X, Probability): 0: (1) × .4^0 × .6^4 = .1296; 1: (4) × .4^1 × .6^3 = .3456; 2: (6) × .4^2 × .6^2 = .3456; 3: (4) × .4^3 × .6^1 = .1536; 4: (1) × .4^4 × .6^0 = .0256;")
Now let’s apply the formula for the probability distribution of a binomial random variable, and see that by using it, we get exactly what we got the long way.
Recall that the general formula for the probability distribution of a binomial random variable with n trials and probability of success p is:
[latex]\mathcal{P}\left(\mathcal{X}=\mathcal{x}\right)=\frac{\mathcal{n}!}{\mathcal{x}!\left(\mathcal{n}-\mathcal{x}\right)!}\mathcal{p}^\mathcal{x}\left(1-\mathcal{p}\right)^{\left(\mathcal{n}-\mathcal{x}\right)}[/latex] for x = 0, 1, 2, 3, … , n
In our case, X is a binomial random variable with n = 4 and p = .4, so its probability distribution is:
[latex]\mathcal{P}\left(\mathcal{X}=\mathcal{x}\right)=\frac{4!}{\mathcal{x}!\left(4-\mathcal{x}\right)!}\left(0.4\right)^\mathcal{x}\left(0.6\right)^{\left(4-\mathcal{x}\right)}[/latex] for x = 0, 1, 2, 3, 4
Let’s use this formula to find P(X = 2) and see that we get exactly what we got before.
[latex]\mathcal{P}\left(\mathcal{X}=2\right)=\frac{4!}{2!\left(4-\mathcal{x}\right)!}\left(0.4\right)^2\left(0.6\right)^{\left(4-2\right)}=\frac{1\times2\times3\times4}{\left(1\times2\right)\left(1\times2\right)}\left(0.4\right)^2\left(0.6\right)^2=0.3456[/latex]
Learn by Doing
Here is another interesting example.
Example
Choosing Numbers at Random
Do people really choose numbers at random?
Each student in a group of 15 students is asked to each pick a number from 1 to 20 completely at random. 3 of the 15 happen to pick the number 7 (this is a probability of .20). Is this an improbably high proportion to choose a particular number?
If the selections are truly random, then each number from 1 to 20, including 7, has probability p = 1/20 = .05 of being selected. The number of trials is n = 15. The probability of at least 3 successes in 15 trials, when each trial has probability of success .05, can be found by applying the binomial formula.
To make the notation easier, we will use a shorthand notation for the number of possible outcomes with x successes out of n. [latex]\frac{\mathcal{n}!}{\mathcal{x}!\left(\mathcal{n}-\mathcal{x}\right)!}[/latex] will be written as: [latex]\left(\begin{matrix}\mathcal{n}\\\mathcal{x}\\\end{matrix}\right)[/latex].
[latex]\mathcal{P}\left(\mathcal{X}\geq3\right)=\mathcal{P}\left(\mathcal{X}=3\right)+\mathcal{P}\left(\mathcal{X}=4\right)+...+\mathcal{P}\left(\mathcal{X}=15\right)\\ =\left(\begin{matrix}15\\3\\\end{matrix}\right)\left(0.05\right)^3\left(0.95\right)^{12}+\left(\begin{matrix}15\\4\\\end{matrix}\right)\left(0.05\right)^4\left(0.95\right)^{11}+...+\left(\begin{matrix}15\\15\\\end{matrix}\right)\left(0.05\right)^{15}\left(0.95\right)^0\\ =.0307+.0049+.0006+...=.0362[/latex]
where all remaining terms after the first 3 are less than .0001. The probability of at least 3 out of 15 people picking 7, when choosing at random from the numbers 1 to 20, is only .0362. Thus, 3 out of 15 is rather improbably high. People may think they are choosing at random, but in fact they tend to favor certain numbers, like the number 7.
Now let’s look at some truly practical applications of binomial random variables.
Example
Airline Flights
Past studies have shown that 90% of the booked passengers actually arrive for a flight. Suppose that a small shuttle plane has 45 seats. We will assume that passengers arrive independently of each other. (This assumption is not really accurate, since not all people travel alone, but we’ll use it for the purposes of our experiment).
Many times airlines “overbook” flights. This means that theairline sells more tickets than there are seats on the plane. This is due to the fact that sometimes passengers don’t show up, and the plane must be flown with empty seats. However, if they do overbook, they run the risk of having more passengers than seats. So, some passengers may be unhappy. They also have the extra expense of putting those passengers on another flight and possibly supplying lodging.
With these risks in mind, the airline decides to sell more than 45 tickets. If they wish to keep the probability of having more than 45 passengers show up to get on the flight to less than 0.05, how many tickets should they sell?
This is a binomial random variable that represents the number of passengers that show up for the flight. It has p = 0.90, and n to be determined.
Suppose theairline sells 50 tickets. Now we have n = 50 and p = 0.90. We want to know P(X > 45), which is 1 – P(X ≤ 45) = 1 – 0.57 or 0.43. Obviously, all the details of this calculation were not shown, since a statistical technology package was used to calculate the answer. This is certainly more than 0.05, so the airline must sell fewer seats.
If we reduce the number of tickets sold, we should be able to reduce this probability. We have calculated the probabilities in the following table:
|
# tickets sold |
P(X > 45) |
|---|---|
|
50 |
0.43 |
|
49 |
0.26 |
|
48 |
0.13 |
|
47 |
0.04 |
|
46 |
0.008 |
From this table, we can see that by selling 47 tickets,the airline can reduce the probability that it will have more passengers show up than there are seats to less than 5%.
Note: For practice in finding binomial probabilities, you may wish to verify one or more of the results from the table above.
Learn by Doing
Mean and Standard Deviation of the Binomial Random Variable
Now that we understand how to find probabilities associated with a random variable X which is binomial, using either its probability distribution formula or software, we are ready to talk about the mean and standard deviation of a binomial random variable. Let’s start with an example:
Example
Blood Type B—Mean
Overall, the proportion of people with blood type B is .1. In other words, roughly 10% of the population has blood type B.
Suppose we sample 120 people at random. On average, how many would you expect to have blood type B?
The answer, 12, seems obvious; automatically, you’d multiply the number of people, 120, by the probability of blood type B, .1. This suggests the general formula for finding the mean of a binomial random variable:
Claim:
If X is binomial with parameters n and p, then
μX=np
Although the formula for mean is quite intuitive, it is not at all obvious what the variance and standard deviation should be. It turns out that:
Claim:
If X is binomial with parameters n and p, then
[latex]\sigma_\mathcal{x}^2=\mathcal{np}\left(1-\mathcal{p}\right);\sigma_\mathcal{x}=\sqrt{\mathcal{np}\left(1-\mathcal{p}\right)}[/latex]
Learn More…
Comment
The binomial mean and variance are special cases of our general formulas for the mean and variance of any random variable.
[latex]\mu\mathcal{x}=\mathcal{x}_1\mathcal{p}_1+\mathcal{x}_2\mathcal{p}_2+...+\mathcal{x}_\mathcal{n}\mathcal{p}_\mathcal{n}=\sum_{\mathcal{i}=1}^{\mathcal{n}}{\mathcal{x}_\mathcal{i}\mathcal{p}_\mathcal{i}}\\ \sigma_\mathcal{x}^2=\left(\mathcal{x}_1-\mu_\mathcal{x}\right)^2\mathcal{p}_1+\left(\mathcal{x}_2-\mu_\mathcal{x}\right)^2\mathcal{p}_2+...+\left(\mathcal{x}_\mathcal{n}-\mu_\mathcal{x}\right)^2\mathcal{p}_\mathcal{n}\\ =\sum_{\mathcal{i}=1}^{\mathcal{n}}\left(\mathcal{x}_\mathcal{i}-\mu_\mathcal{x}\right)^2\mathcal{p}_\mathcal{i}[/latex]
Clearly it is much simpler to use the “shortcut” formulas
[latex]\mu_\mathcal{x}=\mathcal{np}\ and\ \sigma_\mathcal{x}^2=\mathcal{np}\left(1-\mathcal{p}\right);\sigma_\mathcal{x}=\sqrt{\mathcal{np}\left(1-\mathcal{p}\right)}[/latex] than it would be to calculate the mean and variance or standard deviation from scratch.
Example
Blood Type B—Standard Deviation
Suppose we sample 120 people at random. The number with blood type B should be about 12, give or take how many? In other words, what is the standard deviation of the number X who have blood type B?
Since n = 120 and p = .1,
[latex]\sigma_\mathcal{x}^2=120\left(0.1\right)\left(1-0.1\right)=10.8;\sigma_\mathcal{x}=\sqrt{10.8}\approx3.3[/latex]
In a random sample of 120 people, we should expect there to be about 12 with blood type B, give or take about 3.3.
Did I get this?
Learn by Doing
Before we move on to continuous random variables, let’s investigate the shape of binomial distributions. Using the applet below we will see that for different values of n and p, binomial distributions can be symmetric, skewed right or skewed left.
Visit the Learn by Doing link below to complete this exercise.
