4.2: Probability Rules
Basic Probability Rules
Learning Objectives
- Apply probability rules in order to find the likelihood of an event.
- When appropriate, use tools such as Venn diagrams or probability tables as aids for finding probabilities.
In the previous section we considered situations in which all the possible outcomes of a random experiment are equally likely, and learned a simple way to find the probability of any event in this special case. We are now moving on to learn how to find the probability of events in the general case (when the possible outcomes are not necessarily equally likely), using five basic probability rules. Fortunately, these basic rules of probability are very intuitive, and as long as they are applied systematically, they will let us solve more complicated problems; in particular, those problems for which our intuition might be inadequate.
Rule 1 |
|---|
|
For any event A, 0 ≤ P(A) ≤ 1. |
This first rule simply reminds us of the basic property of probability that we’ve already learned. The probability of an event, which informs us of the likelihood of it occurring, can range anywhere from 0 (indicating that the event will never occur) to 1 (indicating that the event is certain). One practical use of this rule is that is can be used to identify any probability calculation that comes out to be more than 1 as wrong.
Before moving on to the other rules, let’s first look at an example that will provide a context for illustrating the next several rules.
Example
As previously discussed, all human blood can be typed as O, A, B or AB. In addition, the frequency of the occurrence of these blood types varies by ethnic and racial groups. According to Stanford University’s Blood Center (bloodcenter.stanford.edu), these are the probabilities of human blood types in the United States (the probability for type A has been omitted on purpose):

Motivating question for rule 2: A person in the United States is chosen at random. What is the probability of the person having blood type A?
Answer: Our intuition tells us that since the four blood types O, A, B, and AB exhaust all the possibilities, their probabilities together must sum to 1, which is the probability of a “certain” event (a person has one of these 4 blood types for certain). Since the probabilities of O, B, and AB together sum to .44 + .1 + .04 = .58, the probability of type A must be the remaining .42 (1 – .58 = .42):

This example illustrates our second rule, which tells us that the probability of all outcomes in the sample space together must be 1.
Rule 2 |
|---|
|
P(S) = 1; that is, the sum of the probabilities of all possible outcomes is 1. |
Comment
This is a good place to compare and contrast what we’re doing here with what we learned in the Exploratory Data Analysis (EDA) section. Notice that in this problem we are essentially focusing on a single categorical variable: blood type. We summarized this variable above, as we summarized single categorical variables in the EDA section, by listing what values the variable takes and how often it takes them. In EDA we used percentages, and here we’re using probabilities, but the two convey the same information. In the EDA section, we learned that a pie chart provides an appropriate display when a single categorical variable is involved, and similarly we can use it here (using percentages instead of probabilities):

Even though what we’re doing here is indeed similar to what we’ve done in the EDA section, there is a subtle but important difference between the underlying situations in this section and the ones in the Exploratory Data Analysis section. In EDA, we summarized data that were obtained from a sample of individuals for whom values of the variable of interest were recorded. Here, when we present the frequency, or probability, of each blood type, we have in mind the entire population of people in the United States, for which we are presuming to know the overall frequency of values taken by the variable of interest.
Did I get this?
Marital status can be categorized into: never married, married, widowedor divorced.
According to Infoplease.com, the following are the probabilities of those marital status categories for adults in the United States (data from 2000):

Let’s move on to rule 3. In probability and in its applications, we are frequently interested in finding out the probability that a certain event will not occur. An important point to understand here is that “event A does not occur” is a separate event that consists of all the outcomes in the sample space S that are not in A. It is for this reason that the event “event A does not occur” is called “the complement event of A,” since it compares event A to the whole sample space. Notation: we will write “not A” to denote the event that A does not occur. Here is a visual representation of how event A and its complement event “not A” together represent the whole sample space.

Comment
Such a visual display is called a “Venn diagram.” A Venn diagram is a simple way to visualize events and the relationships between them using rectangles and circles. We will use Venn diagrams throughout this module.
Rule 3 deals with the relationship between the probability of an event and the probability of its complement event. Given that event A and event “not A” together make up the whole sample space S, and since rule 2 tells us that P(S) = 1, the following rule should be quite intuitive:
Rule 3: The Complement Rule |
|---|
|
P(not A) = 1 – P(A); that is, the probability that an event does not occur is 1 minus the probability that it does occur. |
Example
Back to the blood type example:

Here is some additional information:
- A person with type A can donate blood to a person with type A or AB.
- A person with type B can donate blood to a person with type B or AB.
- A person with type AB can donate blood to a person with type AB only.
- A person with type O blood can donate to anyone.
What is the probability that a randomly chosen person cannot donate blood to everyone? In other words, what is the probability that a randomly chosen person does not have blood type O? We need to find P(not O). Using the Complement Rule, P(not O) = 1 – P(O) = 1 – .44 = .56. In other words, 56% of the U.S. population does not have blood type O:

Comment
Note that the Complement Rule, P(not A) = 1 – P(A) can be re-formulated as P(A) = 1 – P(not A). This seemingly trivial algebraic manipulation has an important application, and actually captures the strength of the complement rule. In some cases, when finding P(A) directly is very complicated, it might be much easier to find P(not A) and then just subtract it from 1 to get the desired P(A). We will come back to this comment and see examples later in this module.
Did I get this?
On the “Information for the Patient” label of a certain antidepressant it is claimed that based on some clinical trials, when taking this medication
– there is a 14% chance of experiencing sleeping problems, or insomnia (denote this event by I)
– there is a 26% chance of experiencing headaches (denote this event by H), and
– there is a 35% chance of experiencing at least one of these two side effects (denote this event by L)
We are now moving to rule 4, which deals with another situation of frequent interest, finding P(A or B), the probability of one event or another occurring. Before we get to the actual rule, however, we need some clarifications and definitions.
When a parent says to his or her child in a toy store “Do you want toy A or toy B?”, this means that the child is going to get only one toy and he or she has to choose between them. Getting both toys is usually not an option.
In contrast,
In probability, “OR” means either one or the other or both.
and so,
P(A or B) = P(event A occurs or event B occurs or both occur)
Having said that, it should be noted that there are some cases where it is simply impossible for the two events to both occur at the same time, in which case we don’t have to worry about the possibility that both occur when we try to find P(A or B). The distinction between events that can happen together and those that cannot is an important one.
Here are two examples:
Example
Consider the following two events:
A—a randomly chosen person has blood type A, and
B—a randomly chosen person has blood type B.
In rare cases, it is possible for a person to have more than one type of blood flowing through his or her veins, but for our purposes, we are going to assume that each person can have only one blood type. Therefore, it is impossible for the events A and B to occur together.
On the other hand …
Example
Consider the following two events:
A—a randomly chosen person has blood type A
B—a randomly chosen person is a woman.
In this case, it is possible for events A and B to occur together.
Definition: Two events that cannot occur at the same time are called disjoint or mutually exclusive. (We will use disjoint.)
We can therefore say that in the first example events A and B are disjoint, and in the second example they are not disjoint. Using Venn diagrams, we can visualize two events that are disjoint and compare them to two events that are not:


The Venn diagrams suggest that another way to think about disjoint versus not disjoint events is that disjoint events do not overlap. They do not share any of the possible outcomes, and therefore cannot happen together. On the other hand, events that are not disjoint are overlapping in the sense that they share some of the possible outcomes and therefore can occur at the same time.
Did I get this?
Recall the couple that is planning to have 3 children, where the sample space S of all possible outcomes is:
S={BBB, BBG, BGB, GBB, GGB, GBG, BGG, GGG}
Consider the following two events:
A—the middle child is a girl
C—the three children are of the same gender

Did I get this?
A couple decides to have children until they have one boy and one girl, but they will not have more than three children. The sample space of possible outcomes is S = {GB, BG, BBG, GGB, BBB, GGG}.
Consider the following events:
A–the couple has one boy
C–the couple has three children
D–all of the children are the same gender
Determine if the following pairs of events are disjoint.
Now that we understand the idea of disjoint events, we can finally get to rule 4. Rule 4 actually has two versions, one for finding P(A or B) in the special case when events A and B are disjoint, and a more general version for when the events are not necessarily disjoint. We will first present the version of rule 4 that is restricted to disjoint events, and later in the module (after rule 5) we will revisit rule 4 and present the more general version.
Rule 4: The Addition Rule for Disjoint Events |
|---|
|
The Addition Rule for Disjoint Events: If A and B are disjoint events, then P(A or B) = P(A) + P(B). |
Comment
When dealing with probabilities, the word “or” will always be associated with the operation of addition; hence the name of this rule, “The Addition Rule.”
Example
Recall the blood type example:

Here is some additional information:
* A person with type A can donate blood to a person with type A or AB.
* A person with type B can donate blood to a person with type B or AB.
* A person with type AB can donate blood to a person with type AB only.
* A person with type O blood can donate to anyone.
What is the probability that a randomly chosen person is a potential donor for a person with blood type A?
From the information given, we know that being a potential donor for a person with blood type A means having blood type A or O. We therefore need to find P(A or O). Since the events A and O are disjoint, we can use the addition rule for disjoint events to get: P(A or O) = P(A) + P(O) = .42 + .44 = .86. It is easy to see why adding the probability actually makes sense. If 42% of the population has blood type A and 44% of the population has blood type O, then 42% + 44% = 86% of the population has either blood type A or O, and thus are potential donors to a person with blood type A. This reasoning about why the addition rule makes sense can be visualized using the pie chart below:

Did I get this?
The probabilities in this table were calculated from data describing the highest level of educational attainment in 2005 for U.S. adults 25 years old or older. (Source: U.S. Census Bureau, Current Population Survey, March 2005)

Practice Activity
So far we have introduced the addition rule for the special case in which the events being considered are disjoint. The purpose of this activity is to make you aware of the danger in wrongly using the addition rule for disjoint events in cases where the events are actually not disjoint. Consider the blood type example again.
Recall the blood type example:

with the following additional information:
A person with type A can donate blood to a person with type A or AB.
A person with type B can donate blood to a person with type B or AB.
A person with type AB can donate blood to a person with type AB only.
A person with type O blood can donate to anyone.
Suppose that there are two patients who are each in need of a blood donation. Patient 1 has blood type A and patient 2 has blood type B. Consider the following events:
D1—a randomly chosen person can be a donor for patient 1.
D2—a randomly chosen person can be a donor for patient 2.
We are interested in finding the probability that a randomly chosen person can be a donor for patient 1 or patient 2. In other words, we are interested in finding P(D1 or D2).
As we mentioned earlier, later on in this module we will establish a more general Addition Rule that applies even when two events are not disjoint.
Comment
The Addition Rule for Disjoint Events can naturally be extended to more than two disjoint events. Let’s take three, for example. If A, B, and C are three disjoint events,

then P(A or B or C) = P(A) + P(B) + P(C). The rule is the same for any number of disjoint events.
Did I get this?
The probabilities in this table were calculated from data describing North America’s favorite car colors in 2003. (Source: DuPont Automotive as cited in money.cnn.com)

We are now done with the first version of the Addition Rule (the version restricted to disjoint events) and we are ready to move on to rule 5. As mentioned before, the general version of the Addition Rule will be presented after rule 5.
Rule 4, the addition rule, deals with finding P(A or B). We are now moving on to rule 5, which deals with yet another situation of frequent interest, finding P(A and B), the probability that both events A and B occur. In other words,
P(A and B) = P(event A occurs and event B occurs)
For example, we might be interested in the probability that if two people are chosen at random, both the first has blood type O and the second has blood type O. Since a person with blood type O can donate blood to anyone, this probability might be of particular interest in this context.
Using a Venn diagram, we can visualize “A and B,” which is represented by the overlap between events A and B:

Comment
There is one special case for which we know what P(A and B) equals without applying any rule.
Did I get this?
So, if events A and B are disjoint, then (by definition) P(A and B)= 0. But what if the events are not disjoint?
Recall that rule 4, the Addition Rule, has two versions. One is restricted to disjoint events, which we’ve already covered, and we’ll deal with the more general version later in this module. The same is true of rule 5. Rule 5 has two versions. The version we’ll present here is restricted to a special case that we’ll now discuss, and there is a more general version that we’ll present in the next module.
The version of rule 5 that will be presented here applies to the special case in which the two events are independent of each other.
- independent
-
Two events A and B are said to be independent if the fact that one event has occurred does not affect the probability that the other event will occur. If whether or not one event occurs does affect the probability that the other event will occur, then the two events are said to be dependent.
Here are a few examples:
Example
A woman’s pocket contains two quarters and two nickels. She randomly extracts one of the coins and, after looking at it, replaces it before picking a second coin.
Let Q1 be the event that the first coin is a quarter and Q2 be the event that the second coin is a quarter.
Are Q1 and Q2 independent events? Yes. Why?
Since the first coin that was selected is replaced, whether or not Q1 occurred (i.e., whether the first coin was a quarter) has no effect on the probability that the second coin will be a quarter, P(Q2). In either case (whether Q1 occurred or not), when she is selecting the second coin, she has in her pocket:

and therefore the P(Q2) = 2/4 = 1/2 regardless of whether Q1 occurred.
Example
A woman’s pocket contains two quarters and two nickels. She randomly extracts one of the coins, and without placing it back into her pocket, she picks a second coin. As before, let Q1 be the event that the first coin is a quarter, and Q2 be the event that the second coin is a quarter.
Are Q1 and Q2 independent events? No. Q1 and Q2 are not independent. They are dependent. Why?
Since the first coin that was selected is not replaced, whether Q1 occurred (i.e., whether the first coin was a quarter) does affect the probability that the second coin is a quarter, P(Q2).
If Q1 occurred (i.e., the first coin was a quarter), then when the woman is selecting the second coin, she has in her pocket:

In this case, P(Q2) = 1/3. However, if Q1 has not occurred (i.e., the first coin was not a quarter, but a nickel), then when the woman is selecting the second coin, she has in her pocket:

In this case, P(Q2) = 2/3.
In these last two examples, we could actually have done some calculation in order to check whether or not the two events are independent or not. Sometimes we can just use common sense to guide us as to whether two events are independent. Here is an example.
Example
Example
Note:
We can generalize what we learned in the last example and say that when two individuals are selected at random from a large population (like in the example, the entire U.S.) any event associated with one individual is independent of any event associated with the other individual. The fact that the two are chosen from a large population is key to the independence.
If we were to change the example to: There are 10 people in a room, 4 of which have blue eyes. Two people are chosen at random. Let B1 be the event that the first person has blue eyes and let B2 be the event that the second person has blue eyes. In this case, since the two are chosen from a group of only 10 (rather than a large population) the events B1 and B2 are not independent. Clearly, whether or not the first person has blue eyes (i.e., whether or not B1 occurs) does have an effect on whether B2 occurs. You will get more practice on this point in the activities below the next comment.
Comment
It is quite common for students to initially get confused about the distinction between the idea of disjoint events and the idea of independent events. The purpose of this comment (and the activity that follows it) is to help students develop more understanding about these very different ideas.
The idea of disjoint events is about whether or not it is possible for the events to occur at the same time (see the examples on page 3 of the Probability Rules section).
The idea of independent events is about whether or not the events affect each other in the sense that the occurrence of one event affects the probability of the occurrence of the other (see the examples above).
The following activity deals with the distinction between these concepts.
The purpose of this activity is to help you strengthen your understanding about the concepts of disjoint events and independent events, and the distinction between them.
Activity
In the following questions, you are presented with a random experiment and two events related to it. You are asked to decide whether the events are disjoint or not, and whether the events are independent or not.
Two people are selected simultaneously and at random from a very large population, and their blood type is checked.
THERE ARE TWO QUESTIONS MISSING THAT RELATE TO EXAMPLES 2 and 3
Let’s summarize the three parts of the activity:
- In Example 1: A and B are not disjoint and independent
- In Example 2: A and B are not disjoint and not independent
- In Example 3: A and B are disjoint and not independent.
Why did we leave out the case when the events are disjoint and independent? The reason is that this case DOES NOT EXIST!
| A and B Independent | A and B Not Independent | |
| A and B Disjoint | DOES NOT EXIST | Example 3 |
| A and B Not Disjoint | Example 1 | Example 2 |
If events are disjoint then they must be not independent (dependent)
Why is that?
Recall: A and B disjoint means that they cannot happen together. In other words, A and B disjoint implies that if event A occurs then B does not and vice versa. Well… if that’s the case, knowing that event A has occurred dramatically changes the likelihood that event B occurs – that likelihood is 0. This implies that A and B are not independent.
Did I get this?
Roughly 7% of American males in U.S. have some sort of color blindness.
Suppose that a medical researcher selects one American male at random.
Let A represent the event ’the selected male is color blind’.
Let B represent the event ’the selected male is not color blind’.
Determine whether A and B are disjoint or independent.
Now, suppose the medical researcher selects two American males at random.
Let A represent the event “the first male is color blind.”
Let B represent the event “the second male is not colorblind.”
Determine whether A and B are disjoint or independent.
Now that we understand the idea of independent events, we can finally get to rule 5. As mentioned before, Rule 5 actually has two versions, one for finding P(A and B) in the special case in which the events A and B are independent, and a more general version for use when the events are not necessarily independent. We will first present the version of rule 5 that is restricted to independent events, and in the next section we will revisit Rule 5 and present the more general version.
Rule 5: The Multiplication Rule for Independent Events |
|---|
|
If A and B are two independent events, then P(A and B) = P(A) * P(B). |
Comment
When dealing with probabilities, the word “and” will always be associated with the operation of multiplication; hence the name of this rule, “The Multiplication Rule.”
Example
Recall the blood type example:

Two people are selected simultaneously and at random from all people in the United States. What is the probability that both have blood type O?
Let O1= “person 1 has blood type O” and
O2= “person 2 has blood type O”
We need to find P(O1 and O2)
Since they were chosen simultaneously and at random, the blood type of one has no effect on the blood type of the other. Therefore, O1 and O2 are independent, and we may apply Rule 5:
P(O1 and O2) = P(O1) * P(O2) = .44 * .44 = .1936.
Did I get this?
A 2011 poll by the Pew Research Center for People and the Press estimated that 62% of U.S. adults favor the death penalty for persons convicted of murder, 31% oppose it, with the remaining 7% undecided.
Let A be the event that the first person supports the death penalty. Let B be the event that the second person supports the death penalty.
We want to find P(A and B). Since the two people are chosen at random from a large population, A and B are independent and we can use the Multiplication Rule for Independent Events.
P(A and B) = P(A) * P(B) = 0.62 * 0.62 = 0.3844
Learn by Doing
Let A be the event that the person voted for Bush in 2000. Let B be the event that the person voted for Bush in 2004. The question asks us to determine P(A and B). We might be tempted to use the Multiplication Rule for Independent Events and write P(A and B) = P(A)*P(B) = 0.48*0.51 = 0.2448, but this would be incorrect because these events are not independent. If an individual voted for Bush in 2000, it is likely that the individual voted for him in 2004. So we are unable to answer the question with the information given.
Did I get this?
Recall the estimate by the Pew Research Center that 62% of U.S. adults favor the death penalty for murder. The same report gave a much lower estimate for the percentage of U.S. college graduates supporting the death penalty in cases of murder. According to census data from 2000, roughly 28% of U.S. adults have a college degree.
What is the probability that a randomly selected U.S. adult has a college degree and favors the death penalty?
Let A be the event that a U.S. adult has a college degree. Let B be the event that this person supports the death penalty. We want to find P(A and B).
So far we have looked at examples where we have to consider and apply only one of the rules. The following example is a case where both the Addition Rule for Disjoint Events and the Multiplication Rule for Independent Events need to be applied in order to find the desired probability.
Example
Recall the blood types example:

Two people are chosen simultaneously and at random. What is the probability that both have the same blood type? For both to have the same blood type there are four possibilities. Both have blood type O or both have blood type A or both have blood type B or both have blood type AB.

In other words, and using our regular notations,
P(same blood type) = P([O1 and O2] or [A1 and A2] or [B1 and B2] or [AB1 and AB2])
Since our four possibilities of both people having the same blood type are disjoint, using our Addition Rule we can add their probabilities (i.e., replace every “or” with +). Also, within each of the four possibilities, we can use the Multiplication Rule and replace “and” with * (using the same independence argument as the first example on this page). Our answer is therefore,

About 38% of the time, two randomly chosen U.S. people would have the same blood type. Note that in this example we used the Addition Rule and the Multiplication Rule one after the other, justifying along the way why it is appropriate to do so.
Did I get this?
Comment
The purpose of this comment is to point out the magnitude of P(A or B) and of P(A and B) relative to either one of the individual probabilities. Since probabilities are never negative, the probability of one event or another is always at least as large as either of the individual probabilities. Since probabilities are never more than 1, the probability of one event and another generally involves multiplying numbers that are less than 1, therefore can never be more than either of the individual probabilities.
Here is an example:
Example
Consider the event A that a randomly chosen person has blood type A. Modify it to a more general event—that a randomly chosen person has blood type A or B—and the probability increases. Modify it to a more specific (or restrictive) event—that not just one randomly chosen person has blood type A, but that out of two simultaneously randomly chosen people, person 1 will have type A and person 2 will have type B—and the probability decreases.
It is important to mention this in order to root out a common misconception. The word “and” is associated in our minds with “adding more stuff.” Therefore, some students incorrectly think that P(A and B) should be larger than either one of the individual probabilities, while it is actually smaller, since it is a more specific (restrictive) event. Also, the word “or” is associated in our minds with “having to choose between” or “losing something,” and therefore some students incorrectly think that P(A or B) should be smaller than either one of the individual probabilities, while it is actually larger, since it is a more general event.
Practically, you can use this comment to check yourself when solving problems. For example, if you solve a problem that involves “or,” and the resulting probability is smaller than either one of the individual probabilities, then you know you have made a mistake somewhere.
Did I get this?
Pick a student at random. Let B denote the event that the student ate breakfast this morning; let M denote the event that the student is male.
As you’ve seen, the last three rules that we’ve introduced (the Complement Rule, the Addition Rule for Disjoint Events, and the Multiplication Rule for Independent Events) are frequently used in solving problems. Before we move on to our next rule, here are two comments that will help you use these rules in broader types of problems and more effectively.
Comment
As we mentioned before, the Addition Rule can be extended to more than two disjoint events. Likewise, the Multiplication Rule can be extended to more than two independent events. So if A, B and C are three independent events, for example, then P(A and B and C) = P(A) * P(B) * P(C). These extensions are quite straightforward, as long as you remember that “or” requires us to add, while “and” requires us to multiply.
An example of a situation where more than two independent events naturally occur is when a random sample of more than two individuals is chosen from a large population.
Here is an example:
Example
Three people are chosen at random from a large population. What is the probability that all three have blood type B? We’ll use the usual notation of B1, B2 and B3 for the events that persons 1, 2 and 3 have blood type B, respectively. We need to find P(B1 and B2 and B3). Let’s solve this one together:
Here is another example that might be quite surprising.
Example
A fair coin is tossed 10 times. Which of the following two outcomes is more likely?
(a) HHHHHHHHHH
(b) HTTHHTHTTH
In fact, they are equally likely. The 10 tosses are independent, so we’ll use the Multiplication Rule for Independent Events:
P(HHHHHHHHHH) = P(H) * P(H) * … *P(H) = 1/2 * 1/2 *… * 1/2 = (1/2)10
P(HTTHHTHTTH) = P(H) * P(T) * … * P(H) = 1/2 * 1/2 *… * 1/2 = (1/2)10
Here is the idea:
My random experiment here is tossing a coin 10 times. You can imagine how huge the sample space is.
There are actually 1,024 possible outcomes to this experiment, all of which are equally likely. Therefore, while it is true that it is more likely to get an outcome that has 5 heads and 5 tails than an outcome that has only heads (since there is only one possible outcome of the latter kind, and many possible outcomes of the former), if I am comparing 2 specific outcomes as I do here, they are equally likely.
Did I get this?
Recall:

Three people are chosen at random. (Assume the choices are independent events). What is the probability that they all have the same blood type?
Comment: Finding the Probability of “At least one of …”
Recall that when we talked about the Complement Rule, we mentioned that we would come back to it later and illustrate its strength. Well, the time has come to do that.
Rule 3: The Complement Rule, P(A) = 1 – P(not A), together with the Multiplication Rule, is extremely useful for finding the probability of events like “at least one of …” in several repetitions of a random experiment.
For example,
- 10 people were randomly chosen. Find P(at least one of the 10 has blood type O).
- A student uses a random guess to answer 10 true/false questions on a test. Find P(the student gets at least one question right).
The key here is to use the fact that the complement event is much easier to deal with than the actual event of interest. Going back to our example:
The complement to “at least one of the 10 has blood type O” is “none of the 10 has blood type O.”
The complement to “getting at least one question right” is “getting none of the questions right.”
(Note how “at least one of” changes to “none” in the complement.)
If you feel unsure about this, go back and redo the “Did I Get This” activity on page 2 of the Probability Rules section.
We’ll start with a very simple example in which it is still manageable to find P(at least one of …) directly, without using the complement rule. Then we’ll alter the example slightly and see how trying to find P(at least one of …) directly can get VERY COMPLICATED, and how the complement rule comes to the rescue. Finally, you’ll check your understanding by attempting to solve a similar problem yourself.
Example
Two people are selected at random. What is the probability that at least one of them has blood type O?
Here is our sample space S = { (O,O) (O, not O) (not O, O) (not O, not O) }
The event “at least one person chosen has blood type O” consists of the first three possible outcomes, and therefore:
P(at least one person chosen has blood type O) = P((O and O) or (O and not O) or (not O and O)) = (.44 * .44) + (.44 * .56) + (.56 * .44) = .6864.
Now we’ll just alter the example slightly by randomly choosing 10 people instead of 2:
Example
A patient with blood type O desperately needs a blood transfusion. Since a person with blood type O can receive blood only from another person who has blood type O, the blood bank decides to choose 10 donors at random and hope that at least one of them has blood type O. Find P(at least one of the 10 donors has blood type O). To make things simpler, let’s denote the event “at least one has blood type O” by L (for at Least).
Solving this using the brute force method would require a prohibitive amount of work. As before, we would need to list all the possible outcomes of blood types of 10 people (using either “O” or “not O”), but this time there are 1,024 of them! We would then need to identify those outcomes that L consists of (i.e., the outcomes in which at least one of the 10 people has blood type O). Next, we would need to find the probability of each of those outcomes and add those probabilities up. What a pain! There must be a better way.
Instead of doing all the work listed above, we can use the Complement Rule, which says P(L) = 1 – P(not L). As we explained before, in this case “not L” is the event “none of the 10 have blood type O,” or in other words that all 10 have a blood type other than O. So we can simply solve (using our regular notation from this module):
P(L) = 1 – P(not L) = 1 – P(not O1 and not O2 and not O3 and not O4 and not O5 and not O6 and not O7 and not O8 and not O9 and not O10). Now, using the multiplication rule, = 1 – (.56 * .56 * .56 * .56 * .56 * .56 * .56 * .56 * .56 * .56) = 1 – .003 = .997.
Therefore, it is almost certain that if we choose 10 people at random, we’ll find that at least one of them has blood type O. This result makes sense, since 44% have blood type O, and so out of 10 people it is almost certain that at least one will have blood type O.
Did I get this?
We are now getting to the last rule in this module in which we’ll go back to P(A or B).
So far, we’ve introduced the Addition Rule for finding P(A or B) in the special case when A and B are disjoint events – that is when the events cannot happen together → P(A and B)= 0.

In this special case P(A or B) refers to the probability of either event A occurring or event B occurring and we said that P(A or B)=P(A) + P(B). Visually, in the Venn diagram above we can clearly see that P(A or B), represented by the total blue area, can be found by adding the areas of the two circles, one representing P(A) and the other P(B).
As we mentioned above the case when A and B are disjoint is a special case and in many situations the events are not disjoint –they can occur at the same time.

We are now ready to learn how to find P(A or B) in this more general case – when A and B are not necessarily disjoint. We’ll call this rule the “General Addition Rule”.
Before we introduce this rule through an example, it is important to understand what P(A or B) represents in the case when A and B are not disjoint. Let’s look at the Venn diagram above.
Again, P(A or B) is represented by the total blue area which in this case looks different. In this case this area includes an overlap between the two circles which corresponds to the probability that both events A and B occur. This difference has an important implication to the meaning of P(A or B) when A and B are not disjoint.
When A and B are not disjoint P(A or B) means P(A occurs or B occurs or both events occur).
Example
It is vital that a certain document reach its destination within one day. To maximize the chances of on-time delivery, two copies of the document are sent using two services, service A and service B. It is known that the probabilities of on-time delivery are:
0.90 for service A (P(A) = 0.90)
0.80 for service B (P(B) = 0.80)
0.75 for both services being on time (P(A and B) = 0.75)
(Note that A and B are not disjoint. They can happen together with probability 0.75.)
The Venn diagrams below illustrate the probabilities P(A), P(B), and P(A and B)
[not drawn to scale]:

In the context of this problem, the obvious question of interest is:
What is the probability of on-time delivery of the document using this strategy (of sending it via both services)?
The document will reach its destination on time as long as it is delivered on time by service A or by service B or by both services. In other words, when event A occurs or event B occurs or both occur. so….
P(on time delivery using this strategy)= P(A or B), which is represented the by the shaded region in the diagram below:

We can now use the three Venn diagrams representing P(A), P(B) and P(A and B) to see that we can find P(A or B) by:
adding P(A) (represented by the left circle) and P(B) (represented by the right circle), then subtracting P(A and B) (represented by the overlap), since we included it twice, once as part of P(A) and once as part of P(B).
This is shown in the following image:

If we apply this to our example, we find that:
P(A or B)= P(on-time delivery using this strategy)= 0.90 + 0.80 – 0.75 = 0.95.
So our strategy of using two delivery services increases our probability of on-time delivery to 0.95.
After this example, the following General Addition Rule for the probability of finding P(A or B), should not be surprising:
Rule 6: The General Addition Rule |
|---|
|
For any 2 events A and B, P(A or B) = P(A) + P(B) – P(A and B). |
Comment:
As we mentioned above P(A or B)= P(A occurs or B occurs or both occur).
Another way to interpret P(A or B) is therefore P(At least one of the two events occur).
Did I get this?
Did I get this?
Suppose that Jim is applying to two colleges: College A, an “Ivy League” school, and College B, a state university. Based on his credentials and the requirements of the two colleges, Jim estimates his chances with the following probabilities:
- Probability that he will be admitted to college A is 0.10.
- Probability that he will be admitted to college B is 0.75.
- Probability that he will be admitted to both colleges is 0.05.
Comments:
- Note that although the motivation for this rule was to find P(A or B) when A and B are not disjoint, this rule is general in the sense that if A and B happen to be disjoint (no overlap), then P(A and B) is zero, and we’re back to the original version of Rule 4, the Addition Rule for Disjoint Events.
- Note that in order to find P(A or B) using the General Addition Rule, you need to know P(A and B), the probability that both events occur. In all three examples above (document delivery, traffic lights and college admittance) P(A and B) was simply given to us. Sometimes instead of giving us P(A and B) directly, we are given a different piece of information which would allow us to find P(A and B). An example of that draws on our previous work with Rule 5. If A and B are independent, then we can multiply the individual probabilities to compute P(A and B)
Did I get this?
What is the probability that at least one of the next two strangers you meet shares your birth month? For this problem assume birth months are equally likely, so the probability of being born in a given month is 1/12 (about 0.083).
Let A = first stranger shares your birth month
Let B = second stranger shares your birth month
Assume that meeting two strangers is like randomly selecting two people from a large population.
Comment:
The words “at least one of” might remind you of the Complement Rule strategy we used on the previous page for finding the probability that “at least one of many independent events occurred.” Note that P(A or B) can also be interpreted as the probability that “at least one of the two events A, B occur.” When the events are independent, the Complement Rule strategy and the General Addition Rule give the same results, as shown below for the birth month problem.
* General Addition Rule when events are independent:
P(at least one of the two shares your birth month)=
P(A or B)=P(A)+P(B)–P(A and B)=
1/12 +1/12 -(1/12)(1/12)=0.16.
* We could also have used the Complement Rule strategy:
P(at least one of the two share your birth month)=
1–P(neither shares your birth month)=
1- (11/12)(11/12)=0.16.
In our delivery example, there are two categorical variables of interest in the background:
- On-time delivery by service A (yes/no)
- On-time delivery by service B (yes/no)
Since each of the two has two possible values (yes/no), there are four possible combinations altogether, which correspond to the four possible outcomes of using the two services.
While the Venn diagrams were great to visualize the General Addition Rule, in cases like these it is much easier to display the information in and work with a two-way table of probabilities, much as we examined the relationship between two categorical variables in the Exploratory Data Analysis section.
How do we build a two-way table of probabilities? Let’s use our delivery example to illustrate this simple process:
Now that we’ve completed the table, it is important to understand what each of the table’s entries mean in context.

Comment
A common mistake is to confuse between: P(A) = P(event A occurs) and P(A and Not B) = P(ONLY event A occurs)[and similarly, between P(B) = P(event B occurs) and P(Not A and B) = P(only event B occurs)].
Looking at the probability table is a great way to clear-up this confusion:

P(A) = 0.90 means that in 90% of the cases when service A is used, it delivers the document on time.
These cases of on-time delivery by service A can be decomposed into two sub-cases:
- P(A and B) = 0.75 → 75% of the time the document is delivered on time also by service B (i.e., the document is delivered on time by both services)
- P(A and Not B) = 0.15 → 15% of the time the document is not delivered on time by service B (i.e., delivered on time only by service A).
Similarly,

P(B) = 0.80 means that in 80% of the cases when service B is used, it delivers the document on time.
These cases of on-time delivery by service B can be decomposed into two sub-cases:
- P(A and B) = 0.75 → 75% of the time the document is delivered on time also by service A (i.e., the document is delivered on time by both services)
- P(Not A and B) = 0.05 → 5% of the time the document is not delivered on time by service A (i.e., delivered on time only by service B).
Example
Recall the smoke detector example from the last activity. Here is a quick recap:
D—the dining room alarm is set off by smoke in the kitchen
B—the bedroom alarm is set off by smoke in the kitchen
P(D) = 0.95
P(B) = 0.40
D and B are independent → P(D and B) = 0.38
Complete the table below. Start with the information that is given and go from there.
Complete the following table: What is the probability that goes in each cell?
| B | not B | Total | |
| D | — 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
— 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
— 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
| not D | — 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
— 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
— 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
| Total | — 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
— 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
— 0.02 0.03 0.05 0.38 0.40 0.57 0.60 0.95 1.00 |
Did I get this?
Did I get this?
Recall the example concerning the delivery of an important document. To maximize the chances of on-time delivery, two copies of the document are sent using two services, service A and service B. It is known that the probabilities of on-time delivery are:
0.90 for service A: P(A) = 0.90
0.80 for service B: P(B) = 0.80
0.75 for both services being on time: P(A and B) = 0.75
Comment
In both the delivery problem and the smoke detector problem, we knew P(A), P(B) and P(A and B). (In the smoke detector problem, we actually needed to work a bit to get P(A and B), but it wasn’t too bad.) Visually, we had the probability for the three shaded cells below, which was enough information to complete the table.

This, however, is not the only combination of three cells that would provide sufficient information to complete the table. Essentially, as long as we are given (or can calculate) one cell in each of the margins (the total row and column), and one of the four cells in the body of the table, we’ll be able to complete the entire table. Visually, we need:

Did I get this?
Researchers studied thousands of court cases. For each case, they recorded the jury’s decision. In addition, they asked the judge in each case how he or she would have decided the same case if there were no jury. In 67% of the cases the jury voted to convict, in 83% of the cases the judge would have convicted, and in 19% of the cases only the judge would have convicted.
Let A be the event “jury convicts”.
Let B be the event “judge convicts”.
Did I get this?
According to www.jointogether.com, in 2000, 87% of all suicides were committed by males, 56% of all suicides were committed using a gun, and 10% of all suicides were committed by women not using a gun.
(We’ll use M for suicide committed by a male, F [= not M] for suicide committed by female, and G for a suicide committed using a gun.)

Comment
When we used two-way tables in the Exploratory Data Analysis (EDA) section, it was to record values of two categorical variables for a concrete sample of individuals. In contrast, the information in a probability two-way table is for an entire population, and the values are rather abstract. If we had treated something like the delivery example in the EDA section, we would have recorded the actual numbers of on-time (and not-on-time) deliveries for samples of documents mailed with service A or B. In this section, the long-term probabilities are presented as being known. Presumably, those probabilities were based on relative frequencies recorded over many repetitions.
Now that we know how to build a two-way probability table, let’s see how we can use information from it to solve problems.
Example
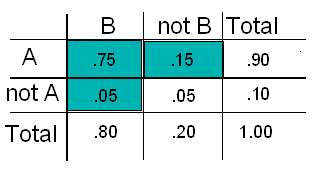
Let’s go back to our delivery example and see how we can “lift” probabilities from the two-way probability table in order to answer the question posed in that example and related questions. Here is the table again:

What is the probability of on-time delivery of the document using the two services strategy?
In other words, what is P(A or B)?
We can use the table in two ways:
(i) We can simply lift P(A), P(B) and P(A and B) from the table as shown in the table below and use the General Addition Rule to get 0.95. as we did before: P(A or B) = P(A) + P(B) − P(A and B) = 0.90 + 0.80 − 0.75 = 0.95.

(ii) Another way to use the table is to use the fact that in probability, “A or B” actually means “A or B or both.” The corresponding cells for these three options are shaded below and are 0.15 (only A), 0.05 (only B), and 0.75 (both). We can add these up to get P(A or B) = 0.95.
Example
What is the probability of on-time delivery by exactly one service?
On-time delivery by exactly one service occurs if the document arrives on-time by service A and not B, or by service B and not A. The probabilities of these two possibilities are represented by the shaded cells in the table below, and are 0.15 and 0.05 respectively. Therefore, P(on-time delivery by exactly one service) = 0.15 + 0.05 = 0.20

Example
What is the probability that the document will not get to its destination on time? This would be the occurrence of the event “not A and not B,” whose probability is 0.05, as shown in the table:

Did I get this?
Candace is applying to two colleges, Ross College and the more prestigious Cirus College. The probability table below represents her belief about whether she will be accepted. We use the following notation:
R—the event of being accepted to Ross College
C—the event of being accepted to Cirus College

We are now done with this section, which introduced various probability rules. Let’s summarize what we’ve learned.
1. The Complement Rule states that
P(not A) = 1 − P(A)
or when rearranged
P(A) = 1 − P(not A).
The Complement Rule is very useful when we need to find probabilities of the sort: P(At least one of several events occur) which is hard to calculate. In this case, we apply the Complement Rule:
P(At least one of several events occur) = 1 − P(None of the events occur), since P(None of the events occur) is usually much easier to find.
2. The General Addition Rule states that for any two events,
P(A or B) = P(A) + P(B) − P(A and B),
where, by P(A or B) we mean P(A occurs or B occurs or both).
In the special case when A and B are disjoint events (which means that P(A and B) = 0), the general addition rule becomes P(A or B) = P(A) + P(B), which we call the Addition Rule for Disjoint Events.
Beware of wrongly using the Addition Rule for Disjoint events when the events are not disjoint.
3. When we want to find P(A and B), we can use the Multiplication Rule, but so far we’ve only learned the restricted version of this rule—the Multiplication Rule for Independent Events. Events are independent if the occurrence of one of the events has no effect on the probability of the other occurring, in which case:
P(A and B) = P(A) * P(B).
4. The Additional Rule for Disjoint Events can be naturally extended to more than two events. In other words, if events A, B, and C are disjoint, then
P(A or B or C)=P(A)+P(B)+P(C).
Similarly, the Multiplication Rule for Independent Events can be naturally extended to more than two independent events. In other words, if events A, B, and C are independent, then P(A and B and C) = P(A) * P(B) * P(C). The same is true for 4, 5, …, disjoint/independent events.
5. When there are two categorical variables in the background, each with two possible values, a two-way probability table is a quick and easy way to display the probabilities associated with the 4 possible combinations.
Conditional Probability and Independence
Learning Objectives
- Explain the reasoning behind conditional probability, and how this reasoning is expressed by the definition of conditional probability.
- Find conditional probabilities and interpret them.
- Determine whether two events are independent or not.
- Use the General Multiplication Rule to find the probability that two events occur (P(A and B)).
- Use probability trees as a tool for finding probabilities.
Introduction
In the last section, we established the five basic rules of probability, which include the two restricted versions of the Addition Rule and Multiplication Rule: The Addition Rule for Disjoint Events and the Multiplication Rule for Independent Events. We have also established a General Addition Rule for which the events need not be disjoint. In order to complete our set of rules, we still require a General Multiplication Rule for which the events need not be independent. In order to establish such a rule, however, we first need to understand the important concept of conditional probability.
This section will be organized as follows: We’ll first introduce the idea of conditional probability, and use it to formalize our definition of independent events, which in the first module was presented only in an intuitive way. We will then develop the General Multiplication Rule, a rule that will tell us how to find P(A and B) in cases when the events A and B are not necessarily independent. We’ll conclude with a discussion of probability trees, a method of displaying conditional probability visually that is very helpful in solving problems.
Learning Objectives
- Explain the reasoning behind conditional probability, and how this reasoning is expressed by the definition of conditional probability.
- Find conditional probabilities and interpret them.
In the first part of this chapter, we’ll introduce the concept of conditional probability. The idea here is that the probabilities of certain events may be affected by whether or not other events have occurred. Let’s illustrate this idea with a simple example:
Example
All the students in a certain high school were surveyed, then classified according to gender and whether they had either of their ears pierced:

(Note that this is a two-way table of counts that was first introduced when we talked about the relationship between two categorical variables. It is not surprising that we are using it again in this example, since we indeed have two categorical variables here: Gender: M or F (in our notation, “not M”), and Pierced: Yes or No)
Suppose a student is selected at random from the school. Let M and not M denote the events of being male and female, respectively, and E and not E denote the events of having ears pierced or not, respectively. We’ll start by asking what will seem like simple questions, and we’ll build our way to conditional probability:
- What is the probability that the student has one or both ears pierced?Since a student is chosen at random from the group of 500 students, out of which 324 are pierced,P(E) = 324/500 = .648
- What is the probability that the student is male?Since a student is chosen at random from the group of 500 students, out of which 180 are male,P(M) = 180/500 = .36
- What is the probability that the student is male and has ear(s) pierced?Since a student is chosen at random from the group of 500 students out of which 36 are male and have their ear(s) pierced, P(M and E) = 36/500 = .072Now something new:
- Given that the student that was chosen is male, what is the probability that he has one or both ears pierced?At this point, new notation is required, to express the probability of a certain event given that another event holds. We will write “the probability of having one or both ears pierced (E) , given that a student is male (M)” as P(E | M).
A word about this new notation: The event whose probability we seek (in this case E) is written first, the vertical line stands for the word “given” or “conditioned on,” and the event that is given (in this case M) is written after the “|” sign.
We call this probability the conditional probability of having one or both ears pierced, given that a student is male: it assesses the probability of having pierced ears under the condition of being male. Now to solve for the probability, we observe that choosing from only the males in the school essentially alters the sample space S from all students in the school to all male students in the school. The total number of possible outcomes is no longer 500, but has changed to 180. Out of those 180 males, 36 have ear(s) pierced, and thus:
P(E | M) = 36/180 = .20.
A good visual illustration of this conditional probability is provided by the two-way table:

which shows us that conditional probability is not very different from (and actually quite the same as) the conditional percents we calculated in the example above.
Did I get this?
Consider the piercing example, where the following two-way table is given,

Recall also that M represents the event of being a male (“not M” represents being a female), and E represents the event of having one or both ears pierced.
Another way to visualize conditional probability is using a Venn diagram:

In both the two-way table and the Venn diagram, the reduced sample space (comprised of only males) is shaded light green, and within this sample space, the event of interest (having ears pierced) is shaded darker green. The two-way table illustrates the idea via counts, while the Venn diagram converts the counts to probabilities, which are presented as regions rather than cells.
We may work with counts, as presented in the two-way table, to write
P(E | M) = 36/180.
Or we can work with probabilities, as presented in the Venn diagram, by writing
P(E | M) = (36/500) / (180/500).
We will want, however, to write our formal expression for conditional probabilities in terms of other, ordinary, probabilities and therefore the definition of conditional probability will grow out of the Venn diagram.
Notice that
P(E | M) = (36/500) / (180/500) = P(M and E) / P(M). Generalized, we have a formal definition of conditional probability:
- conditional probability
-
The conditional probability of event B, given event A, is P(B | A) = P(A and B) / P(A)
Comments
- Note that when we evaluate the conditional probability, we always divide by the probability of the given event. The probability of both goes in the numerator.
- The above formula holds as long as P(A) > 0, since we cannot divide by 0. In other words, we should not seek the probability of an event given that an impossible event has occurred.
Let’s see how we can use this formula in practice:
Example
(a) Suppose that the patient experiences insomnia; what is the probability that the patient will also experience headache?
Since we know (or it is given) that the patient experienced insomnia, we are looking for P(H | I). According to the definition of conditional probability:
P(H | I) = P(H and I) / P(I) = .05/.14 = .357.
(b) Suppose the drug induces headache in a patient; what is the probability that it also induces insomnia?
Here, we are given that the patient experienced headache, so we are looking for P(I | H).
Using the definition P(I | H) = P(I and H) / P(H) = .05/.26 = .1923.
Comment
Note that the answers to (a) and (b) above are different. In general, P(A | B) does not equal P(B | A). We’ll come back and illustrate this point later in this module.
The purpose of the following activity is to give you guided practice in using the definition of conditional probability, and teach you how the Complement Rule works with conditional probability.
Did I get this?
Recall the delivery services example:
It is vital that a certain document reach its destination within one day. To maximize the chances of on-time delivery, two copies of the document are sent using two services, service A and service B, and the following probability table summarizes the chances of on-time delivery:

Did I get this?
Recall the smoke alarms example from the previous module. A homeowner has smoke alarms installed in the dining room (adjacent to the kitchen) and an upstairs bedroom (above the kitchen). The two-way table below shows probabilities of smoke in the kitchen triggering the alarm in the dining room (D) or not, and in the bedroom (B) or not. Use this two-way table to answer the following:

Learning Objectives
- Determine whether two events are independent or not.
As we saw in the Exploratory Data Analysis section, whenever a situation involves more than one variable, it is generally of interest to determine whether or not the variables are related. In probability, we talk about independent events, and in the first module we said that two events A and B are independent if event A occurring does not affect the probability that event B will occur. Now that we’ve introduced conditional probability, we can formalize the definition of independence of events and develop four simple ways to check whether two events are independent or not. We will introduce these “independence checks” using examples, and then summarize.
Example
Consider again the two-way table for all 500 students in a particular high school, classified according to gender and whether or not they have one or both ears pierced.

If the two are equal (i.e., knowing or not knowing whether A has occurred has no effect on the probability of B occurring) then the two events are independent. Otherwise, if the probability changes depending on whether we know that A has occurred or not, then the two events are not independent. Similarly, using the same reasoning, we can compare P(A | B) and P(A).
Example
Recall the side effects example. On the “Information for the Patient” label of a certain antidepressant it is claimed that based on some clinical trials, there is a 14% chance of experiencing sleeping problems known as insomnia (denote this event by I), there is a 26% chance of experiencing headache (denote this event by H), and there is a 5% chance of experiencing both side effects (I and H).
Are the two side effects independent of each other?
To check whether the two side effects are independent, let’s compare P(H | I) and P(H).
In the previous part of this module, we found that P(H | I) = P(H and I) / P(I) = .05/.14 = .357, while P(H) = .26. Knowing that a patient experienced insomnia increases the likelihood that he/she will also experience headache from .26 to .357. The conclusion, therefore is that the two side effects are not independent, they are dependent.
Alternatively, we could have compared P(I | H) to P(I). P(I) = .14, and previously we found that P(I | H) = P(I and H) / P(H) = .05/.26 = .1923, and again, since the two are not equal, we can conclude that the two side effects I and H are dependent.
Did I get this?
Recall again the smoke alarms example.
A homeowner has smoke alarms installed in the dining room (adjacent to the kitchen) and an upstairs bedroom (above the kitchen). The two-way table below shows probabilities of smoke in the kitchen triggering the alarm in the dining room (D) or not, and in the bedroom (B) or not.

Comment
Recall the pierced ears example. We checked the independence of the events M (being a male) and E (having pierced ears) by comparing P(E) to P(E | M).
An alternative method of checking for dependence would be to compare P(E | M) with P(E | not M) [same as P(E | F)]. In our case, P(E | M) = 36/180 = .2, while P(E | not M) = 288/320 = .9, and since the two are very different, we can say that the events E and M are not independent.
In general, another method for checking the independence of events A and B is to compare P(B | A) and P(B | not A). In other words, two events are independent if the probability of one event does not change whether we know that the other event has occurred or we know that the other event has not occurred. It can be shown that P(B | A) and P(B | not A). would differ whenever P(B) and P(B | A) differ, so this is another perfectly legitimate way to establish dependence or independence.
Did I get this?
Recall again the smoke alarms example.
A homeowner has smoke alarms installed in the dining room (adjacent to the kitchen) and an upstairs bedroom (above the kitchen). The two-way table below shows probabilities of smoke in the kitchen triggering the alarm in the dining room (D) or not, and in the bedroom (B) or not.

Before we establish a general rule for independence, let’s consider an example that will illustrate another method that we can use to check whether two events are independent:
Example
A group of 100 college students were surveyed about their gender and whether they had decided on a major.

Offhand, we wouldn’t necessarily have any compelling reason to expect that deciding on a major would depend on a student’s gender. We can check for independence by comparing the overall probability of being decided to the probability of being decided given that a student is female:
P(D) = 45/100 = .45 and P(D | F) = 27/60 = .45.
The fact that the two are equal tells us that, as we might expect, deciding on a major is independent of gender. Note from the comment that these must also equal P(D | M), which is 18/40 = .45.
Now let’s approach the issue of independence in a different way: first, we may note that the overall probability of being decided is 45/100 = .45.

And the overall probability of being female is 60/100 = .60.

If being decided is independent of gender, then 45% of the 60% of the class who are female should have a decided major; in other words, the probability of being female and decided should equal the probability of being female multiplied by the probability of being decided. If the events F and D are independent, we should have P(F and D) = P(F) * P(D).
In fact, P(F and D) = 27/100 = .27 = P(F) * P(D) = .45 * .60. This confirms our alternate verification of independence.
In general, another method for checking the independence of events A and B is to compare P(A and B) to P(A) * P(B). If the two are equal, then A and B are independent, otherwise the two are not independent.
Let’s summarize all the possible methods we’ve seen for checking the independence of events in one rule:
Two events A and B are independent if any one of the following hold:
P(B | A) = P(B)
P(A | B) = P(A)
P(B | A) = P(B | not A)
P(A and B) = P(A) * P(B)
Comment
These various equalities turn out to be equivalent, so that if one equality holds, all are equal, and if one equality does not hold, all are not equal. (This is the case for the same reason that knowing one of the values P(A and B), P(A and not B), P(not A and B), or P(not A and not B), along with P(A) and P(B), allows you to determine the remaining cells of a two-way probability table.)
Therefore, in order to check whether events A and B are independent or not, it is sufficient to check only whether one of the four equalities holds—whichever is easiest for you.
The purpose of the next activity is to practice checking the independence of two events using the four different possible methods that we’ve provided, and see that all of them will lead us to the same conclusion, regardless of which of the four methods we use.
Did I get this?
Recall the delivery services example:
It is vital that a certain document reach its destination within one day. To maximize the chances of on-time delivery, two copies of the document are sent using two services, service A and service B, and the following probability table summarizes the chances of on-time delivery:

Are the delivery times of the two services independent? In other words, are the events A and B independent? Common sense would say that there will be some degree of dependence between A and B, since the reasons that would cause one service to be delayed (like bad weather, airport delays, etc), would most likely also affect the other service, and cause it to be delayed too. Let’s review the four possible methods that we can use to check whether events A and B are independent:
Two events A and B are independent if any one of the following hold:
P(B | A) = P(B)
P(A | B) = P(A)
P(B | A) = P(B | not A)
P(A and B) = P(A) * P(B)
Use the four different methods to check whether events A and B are independent, and see that indeed all four are leading you to the same conclusion.
Learning Objectives
- Use the General Multiplication Rule to find the probability that two events occur (P(A and B)).
Now that we have an understanding of conditional probabilities and can express them with concise notation, and have a more formal understanding of what it means for two events to be independent, we can finally establish the General Multiplication Rule, a formal rule for finding P(A and B) that applies to any two events, whether they are independent or dependent.
We begin with an example that contrasts P(A and B) for independent and dependent cases.
Example
Suppose you pick two cards at random from four cards consisting of one of each suit: club, diamond, heart, and spade, where the first card is replaced before the second card is picked. What is the probability of picking a club and then a diamond? Because the sampling is done with replacement, whether or not a diamond is picked on the second selection is independent of whether or not a club has been picked on the first selection. Rule 5, the multiplication rule for independent events, tells us that:
P(C1 and D2) = P(C1) * P(D2) = 1/4 * 1/4 = 1/16.
[Here we denote the event “club picked on first selection” as C1 and the event “diamond picked on second selection” as D2.] The display below shows that 1/4 of the time we’ll pick a club first, and of these times, 1/4 will result in a diamond on the second pick: 1/4 * 1/4 = 1/16 of the selections will have a club first and then a diamond.

Example
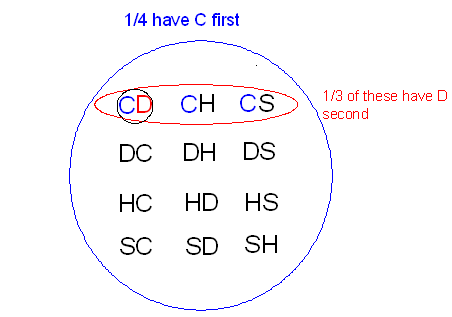
Suppose you pick two cards at random from four cards consisting of one of each suit: club, diamond, heart, and spade, without replacing the first card before the second card is picked. What is the probability of picking a club and then a diamond? The probability in this case is not 1/4 * 1/4 = 1/16; because the sampling is done without replacement, so whether or not a diamond is picked on the second selection does depend on what was picked on the first selection. (For instance, if a diamond was picked on the first selection, the probability of another diamond is zero!) As in the example above, 1/4 of the time we’ll pick a club first. But since the club has been removed, 1/3 of these selections with a club first will have a diamond second. The probability of a club and then a diamond is 1/4*1/3=1/12; this is the probability of getting a club first, multiplied by the probability of getting a diamond second, given that a club was picked first. Using the notation of conditional probabilities, we can write
P(C1 and D2) = P(C1) * P(D2 | C1) = 1/4 * 1/3 = 1/12.
For independent events A and B, we had the rule P(A and B) = P(A) * P(B). Due to independence, to find the probability of both, we could multiply the probability of A by the simple probability of B, because the occurrence of A would have no effect on the probability of B occurring. Now, for events A and B that may be dependent, to find the probability of both, we multiply the probability of A by the conditional probability of B, taking into account that A has occurred. Thus, our general multiplication rule is stated as follows:
|
The General Multiplication Rule: For any two events A and B, P(A and B) = P(A) * P(B | A) |
Here, again, is the General Multiplication Rule:
For any two events A and B, P(A and B) = P(A) * P(B | A)
Comments
- Note that although the motivation for this rule was to find P(A and B) when A and B are not independent, this rule is general in the sense that if A and B happen to be independent, then P(B | A) = P(B) is true, and we’re back to Rule 5—the Multiplication Rule for Independent Events: P(A and B) = P(A) * P(B).
- The General Multiplication Rule is just the definition of conditional probability in disguise. Recall the definition of conditional probability: P(B | A) = P(A and B) / P(A) Let’s isolate P(A and B) by multiplying both sides of the equation by P(A), and we get: P(A and B) = P(A) * P(B | A). That’s it … this is the General Multiplication Rule.
- The General Multiplication Rule is useful when two events, A and B, occur in stages, first A and then B (like the selection of the two cards in the previous example). Thinking about it this way makes the General Multiplication Rule very intuitive. For both A and B to occur you first need A to occur (which happens with probability P(A)), and then you need B to occur, knowing that A has already occurred (which happens with probability P(B | A)).
Did I get this?
A woman’s pocket contains 2 quarters and 2 nickels; she randomly extracts one of the coins, and without replacing it picks a second coin.
Let’s look at another, more realistic example:
Example
In a certain region, one in every thousand people (0.001) of all individuals are infected by the HIV virus that causes AIDS. Tests for presence of the virus are fairly accurate but not perfect. If someone actually has HIV, the probability of testing positive is .95. Let H denote the event of having HIV, and T the event of testing positive.
(a) Express the information that is given in the problem in terms of the events H and T.
“one in every thousand people (0.001) of all individuals are infected with HIV” → P(H) = .001
“If someone actually has HIV, the probability of testing positive is .95” → P(T | H) = .95
(b) Use the General Multiplication Rule to find the probability that someone chosen at random from the population has HIV and tests positive.
P(H and T) = P(H) * P(T | H) = .001*.95 = .00095.
(c) If someone has HIV, what is the probability of testing negative? Here we need to find P(not T | H).
Recall from an activity earlier in this module that the Complement Rule works with conditional probabilities as long as we condition on the same event, therefore: P(not T | H) = 1 – P(T | H) = 1 – .95 = .05.

