4.1: Probability Basics
Learning Objective
- Relate the probability of an event to the likelihood of this event occurring.
Defining Probability
Now that we understand how probability fits into the Big Picture as a key element behind statistical inference, we are ready to learn more about it. Our first goal is to introduce some fundamental terminology (the language) and notation that is used when discussing probability. Before we do that, though, let’s start with two fun examples that explain the reasons for the careful treatment that we give probability in this course.
Often, relying only on our intuition is not sufficient to determine probability, so we need some tools to work with, which is exactly what we study in this section.
Here are two examples:
Example
The Let’s Make a Deal Paradox
Let’s Make a Deal was a popular television game show, which first aired in the 1960s. The Let’s Make a Deal paradox is named after that show. In the show, the contestant had to choose between three doors. One of the doors had a big prize behind it such as a car or a lot of cash, and the other two were empty. (Actually, for entertainment’s sake, each of the other two doors had some stupid gift behind it, like a goat or a chicken, but we’ll refer to them here as empty.)
The contestant had to choose one of the three doors, but instead of revealing the chosen door, the host revealed one of the two unchosen doors to be empty. At this point in the game, there were two unopened doors: the door that the contestant had originally chosen and the remaining unchosen door. One of them had the prize behind it.
The contestant was given the option either to stay with the door that he or she had initially chosen or switch to the other door.
What do you think the contestant should do, stay or switch? What do you think is the probability that you will win the big prize if you stay? What about if you switch?
In order for you to gain a feel for this game, you can play it a few times using this exercise.
How it works:
In a popular game show, contestants are asked to choose one of three doors. Behind one is a fabulous prize! Behind the others are gag gifts. When you choose a door, the game show host shows you a gag gift behind one of the two doors not chosen. You are given the option of switching to the one remaining door or staying with your original choice. Which is the better strategy: switch or stay? You choose doors by clicking on a door. A gag gift (represented by a donkey) is then revealed behind one of the doors you did not select. Click on your original door to stay, or click on the other unopened door to switch. Then all the doors are opened. Did you win? The table keeps track of your wins and losses using each strategy.
Learn by Doing
If you are still not convinced (or even if you are), here is a different way of explaining the paradox:
Example
The Birthday Problem
Suppose that you are at a party with 59 other people (for a total of 60). What are the chances (or, what is the probability) that at least 2 of the 60 guests share the same birthday?
To clarify, by “share the same birthday,” we mean that 2 people were born on the same date, not necessarily in the same year. Also, for the sake of simplicity, ignore leap years, and assume that there are 365 days in each year.
Learn by Doing
Indeed, there is a 99.4% chance that at least 2 of the 60 guests share the same birthday. In other words, it is almost certain that at least 2 of the guests share the same birthday. This is very counterintuitive.
Unlike the Let’s Make a Deal example, for this scenario, we don’t really have a good step-by-step explanation that will give you insight into this surprising answer. Later in this section, we will revisit this example and explain the solution.
From these two examples, you have seen that your original hunches cannot always be counted upon to give you correct predictions of probabilities.
In general, probability is not always intuitive.
Even though these two examples are definitely from the “harder” end of the complexity spectrum, hopefully they have motivated you to learn more about probability. We will need to further expand and extend our understanding of probability. Eventually we will need to develop a more formal approach to probability, but we will begin with an informal discussion of what probability is.
What is Probability?
Probability is a mathematical description of randomness and uncertainty. It is a way to measure or quantify uncertainty. Another way to think about probability is that it is the official name for “chance.”
Probability is the Likelihood of Something Happening
One way to think of probability is that it is the likelihood that something will occur.
Probability is used to answer the following types of questions:
-
What is the chance that it will rain tomorrow?
-
What is the chance that a stock will go up in price?
-
What is the chance that I will have a heart attack?
-
What is the chance that I will live longer than 70 years?
- What is the likelihood that when rolling a pair of dice, I will roll doubles?
- What is the probability that I will win the lottery?
Each of these examples has some uncertainty. For some, the chances are quite good, so the probability would be quite high. For others, the chances are not very good, so the probability is quite low (especially winning the lottery).
Certainly, the chance of rain is different each day, and is higher during some seasons. Your chance of having a heart attack, or of living longer than 70 years, depends on things like your current age, your family history, and your lifestyle. However, you could use your intuition to predict some of those probabilities fairly accurately, while others you might have no hunches about at all.
Notation
We think you will agree that the word probability is a bit long to include in equations, graphs and charts, so it is customary to use some simplified notation instead of the entire word.
If we wish to indicate “the probability it will rain tomorrow,” we use the notation “P(rain tomorrow).” We can abbreviate the probability of anything. If we let A represent what we wish to find the probability of, then P(A) would represent that probability.
We can think of “A” as an “event.”
| NOTATION | MEANING |
|---|---|
| P(win lottery) | the probability that a person who has a lottery ticket will win that lottery |
| P(A) | the probability that event A will occur |
| P(B) | the probability that event B will occur |
| Principle |
|---|
|
The “probability” of an event tells us how likely it is that the event will occur. |
What values can the probability of an event take, and what does the value tell us about the likelihood of the event occurring?
Exercise
| Principle |
|---|
|
The probability that an event will occur is between 0 and 1 or 0 ≤ P(A) ≤ 1. |
Many people prefer to express probability in percentages. Since all probabilities are decimals, each can be changed to an equivalent percentage. Thus, the latest principle is equivalent to saying, “The chance that an event will occur is between 0% and 100%.”
Probabilities can be determined in two fundamental ways. Keep reading to find out what they are.
Determining Probability
There are 2 fundamental ways in which we can determine probability:
-
Theoretical (also known as Classical)
-
Empirical (also known as Observational)
Classical methods are used for games of chance, such as flipping coins, rolling dice, spinning spinners, roulette wheels, or lotteries.
They are “classical” because their values are determined by the game itself.
Example
Flipping a Fair Coin
A coin has two sides; we usually call them “heads” and “tails.” For a “fair” coin (one that is not unevenly weighted, and does not have identical images on both sides) the chances that a “flip” will result in either side facing up are equally likely. Thus, P(heads) = P(tails) = 1/2 or 0.5. Letting H represent “heads,” we can abbreviate the probability: P(H) = 0.5.
Classical probabilities can also be used for more realistic and useful situations. A practical use of a coin flip would be for you and your roommate to decide randomly who will go pick up the pizza you ordered for dinner. A common expression is “Let’s flip for it.” This is because a coin can be used to make a random choice with two options. Many sporting events begin with a coin flip to determine which side of the field or court each team will play on, or which team will have control of the ball first.
Example
Rolling Fair Dice
Each traditional (cube-shaped) die has six sides, marked in dots with the numbers 1 through 6. On a “fair” die, these numbers are equally likely to end up face-up when the die is rolled. Thus, P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = 1/6 or about 0.167.
Here, again, is a practical use of classical probability. Suppose six people go out to dinner. You want to randomly decide who will pick up the check and pay for everyone. Again, the P(each person) = 1/6.
Example
Spinners
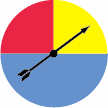
This particular spinner has three colors, but each color is not equally likely to be the result of a spin, since the portions are not the same size.
Since the blue is half of the spinner, P(blue) = 1/2. The red and yellow make up the other half of the spinner and are the same size. Thus, P(red) = P(yellow) = 1/4.
Suppose there are 2 freshmen, 1 sophomore, and one junior in a study group. You want to select one person. The P(F) = 2/4 = 1/2; P(S) = 1/4; and P(J) = 1/4, just like the spinner.
Example
Selecting Students
Suppose we had three students and wished to select one of them randomly. To do this you might have each person write his/her name on a (same-sized) piece of paper, then put the three papers in a hat, and select one paper from the hat without looking.
Since we are selecting randomly, each is equally likely to be chosen. Thus, each has a probability of 1/3 of being chosen.
A slightly more complicated, but more interesting, probability question would be to propose selecting 2 of the students pictured above, and ask, “What is the probability that the two students selected will be different genders?”
We will now shift our discussion to empirical ways to determine probabilities.
A Question
A single flip of a coin has an uncertain outcome. So, every time a coin is flipped, the outcome of that flip is unknown until the flip occurs.
However, if you flip a fair coin over and over again, would you expect P(H) to be exactly 0.5? In other words, would you expect there to be the same number of results of “heads” as there are “tails”?
After doing this experiment, an important question naturally comes to mind. How would we know if the coin was not fair? Certainly, classical probability methods would never be able to answer this question. In addition, classical methods could never tell us the actual P(H). The only way to answer this question is to perform another experiment.
So, these types of experiments can verify classical probabilities and they can also determine when games of chance are not following fair practices. However, their real importance is to answer probability questions that arise when we are faced with a situation that does not follow any pattern and cannot be predetermined. In reality, most of the probabilities of interest to us fit the latter description.
To Summarize
- Probability is a way of quantifying uncertainty.
- We are interested in the probability of an event—the likelihood of the event occurring.
- The probability of an event ranges from 0 to 1. The closer the probability is to 0, the less likely the event is to occur. The closer the probability is to 1, the more likely the event is to occur.
- There are two ways to determine probability: Theoretical (Classical) and Empirical (Observational).
- Theoretical methods use the nature of the situation to determine probabilities.
- Empirical methods use a series of trials that produce outcomes that cannot be predicted in advance (hence the uncertainty)
Relative Frequency Probability
Learning Objective
- Explain how relative frequency can be used to estimate the probability of an event.
If we toss a coin, roll a die, or spin a spinner many times, we hardly ever achieve the exact theoretical probabilities that we know we should get, but we can get pretty close. When we run a simulation or when we use a random sample and record the results, we are using empirical probability. This is often called the Relative Frequency definition of probability.
Here is a realistic example where the relative frequency method was used to find the probabilities:
Example
Blood Type
Researchers discovered at the beginning of the 20th century that human blood comes in various types (A, B, AB, and O), and that some types are more common than others. How could researchers determine the probability of a particular blood type, say O? Just looking at one or two or a handful of people would not be very helpful in determining the overall chance that a randomly chosen person would have blood type O. But sampling many people at random, and finding the relative frequency of blood type O occurring, provides an adequate estimate. For example, it is now well known that the probability of blood type O among white people in the United States is 0.45. This was found by sampling many (say, 100,000) white people in the country, finding that roughly 45,000 of them had blood type O, and then using the relative frequency: 45,000 / 100,000 = 0.45 as the estimate for the probability for the event “having blood type O.”
(Comment: Note that there are racial and ethnic differences in the probabilities of blood types. For example, the probability of blood type O among black people in the United States is 0.49, and the probability that a randomly chosen Japanese person has blood type O is only 0.3).
Let’s review the relative frequency method for finding probabilities:
To estimate the probability of event A, written P(A), we may repeat the random experiment many times and count the number of times event A occurs. Then P(A) is estimated by the ratio of the number of times A occurs to the number of repetitions, which is called the relative frequency of event A.
Did I get this?
What are the breakfast-eating habits of college students?
A group of 460 college students was surveyed over several typical weekdays, and 253 of them reported that they had eaten breakfast that day. Let B be the event of interest—that a college student eats breakfast.
So, we’ve seen how the relative frequency idea works, and the relative frequency of an event does indeed approach the theoretical probability of that event as the number of repetitions increases. This is called the Law of Large Numbers.
The Law of Large Numbers states that as the number of trials increases, the relative frequency becomes the actual probability. So, using this law, as the number of trials increases, the empirical probability gets closer and closer to the theoretical probability.
| Principle |
|---|
|
Law of Large Numbers: The actual (or true) probability of an event (A) is estimated by the relative frequency with which the event occurs in a long series of trials. |
Comments:
- Note that the relative frequency approach provides only an estimate of the probability of an event. However, we can control how good this estimate is by the number of times we repeat the random experiment. The more repetitions that are performed, the closer the relative frequency gets to the true probability of the event.
- One interesting question would be: “How many times do I need to repeat the random experiment in order for the relative frequency to be, say, within .001 of the actual probability of the event?” We will come back to that question in the inference section.
- A pedagogical comment: We’ve introduced relative frequency here in a more practical approach, as a method for estimating the probability of an event. More traditionally, relative frequency is not presented as a method, but as a definition:
- Relative Frequency: The probability of an event (A) is the relative frequency with which the event occurs in a long series of trials.
- There are many situations of interest in which physical circumstances do not make the probability obvious. In fact, most of the time it is impossible to find the theoretical probability, and we must use empirical probabilities instead.
Sample Space and Events
Learning Objective
As we saw in the previous section, probability questions arise when we are faced with a situation that involves uncertainty. Such a situation is called a random experiment, an experiment that produces an outcome that cannot be predicted in advance (hence the uncertainty).
Here are a few examples of random experiments:
-
Toss a coin once and record whether you get heads (H) or tails (T). The possible outcomes that this random experiment can produce are: {H, T}.
- Toss a coin twice. The possible outcomes that this random experiment can produce are: {HH, HT, TH, TT}.
- Toss a coin 3 times. The possible outcomes in this case are: {HHH, THH, HTH, HHT, HTT, THT, TTH, TTT}.
- Toss a coin until you get the first tails (T). When we conduct this experiment, one possible outcome is that we get T in the first toss and we are done. Another possible outcome is that we get H in the first toss, toss a second time, get T and be done. We might need three tosses until we get the first T, etc. The possible outcomes of this random experiment are therefore: {T, HT, HHT, HHHT, …}. (Note that in this example the list of possible outcomes is not finite as in examples 1-3. This is not an important distinction at this point, just a noteworthy observation.)
- Choose a person at random and check his or her blood type. In this random experiment the possible outcomes are the four blood types: {A, B, AB, O}.
- There are two job openings for a staff position at a certain college, and 4 equally qualified candidates for the job (Ann, Beth, Jim and Dan). For fairness, the human resources department decides to choose two of the four candidates at random. The possible outcomes of this random experiment are all possible pairs of candidates: { (Ann, Beth), (Ann, Jim), (Ann, Dan), (Beth, Jim), (Beth, Dan), (Jim, Dan) }.
Comment: Does Order Matter?
Note that when a coin is tossed twice, as in example 2, the possible outcome HT (indicating that the first toss was H and the second T) is NOT the same as the outcome TH (indicating that T occurred first and then H), and therefore both outcomes were listed separately. This is an example of a situation when order does matter. However, order does not always matter. Example 6 is a case in which order does not matter. The outcome (Ann, Beth) indicates that Ann and Beth are the two randomly chosen to get the jobs. Whether Ann appears first or Beth does is irrelevant in this case, and therefore (Beth, Ann) was not listed as a separate outcome.
There is really no rule that dictates when order matters and when it doesn’t. It is sometimes clear from the way the random experiment is defined. For example, suppose I were to change example 6 slightly:
There are two job openings for similar staff positions at a certain college: one in the Registrar’s Office, and one in the Office of Admissions. The Human Resources Department has identified four equally qualified candidates for the jobs (Ann, Beth, Jim and Dan), and for fairness decides to choose two of the four candidates at random. The first chosen will fill the position in the Registrar’s Office, and the second will fill the position in the Office of Admissions.
Now order is relevant—the two outcomes (Ann, Beth) and (Beth, Ann) are not the same in this scenario. The first outcome indicates that Ann got the position at the Registrar’s Office and Beth got the position at the Office of Admissions, while the second outcome indicates the reverse. In this case, therefore, all the possible outcomes are:
{ (Ann, Beth), (Beth, Ann), (Ann, Jim), (Jim, Ann), (Ann, Dan), (Dan, Ann),
(Beth, Jim), (Jim, Beth), (Beth, Dan), (Dan, Beth), (Jim, Dan), (Dan, Jim) }
Each random experiment has a set of possible outcomes, and there is uncertainty as to which of the outcomes we are actually going to get once the experiment is conducted. This list of possible outcomes is called the sample space of the random experiment, and is denoted by the (capital) letter S.
Going back to the 6 examples above, we can write:
Example 1: S = {H, T}
Example 2: S = {HH, HT, TH, TT}
Example 3: S = {HHH, THH, HTH, HHT, HTT, THT, TTH, TTT}
Example 4: S = {T, HT, HHT, HHHT, …}
Example 5: S = {A, B, AB, O}
Example 6: S = { (Ann, Beth), (Ann, Jim), (Ann, Dan), (Beth, Jim), (Beth, Dan), (Jim, Dan) }.
Did I get this?
In each of the following situations, choose the correct sample space (S) for the random experiment that is described.
So far, we have a random experiment and its sample space—the set of all possible outcomes it can produce. Where does probability come into the picture?
Once we have defined a random experiment, we can talk about an event of interest, which is a statement about the nature of the outcome that we’re actually going to get once the experiment is conducted. Events are denoted by capital letters (other than S, which is reserved for the sample space).
Example
Tossing a Coin 3 Times
Consider example 3, tossing a coin three times. Recall that the sample space in this case is:
S = {HHH, THH, HTH, HHT, HTT, THT, TTH, TTT}
We can define the following events:
Event A: “Getting no H”
Event B: “Getting exactly one H”
Event C: “Getting at least one H”
Note that each event is indeed a statement about the outcome that the experiment is going to produce.
In practice, each event corresponds to some collection (subset) of the outcomes in the sample space:
Event A: “Getting no H” → TTT
Event B: “Getting exactly one H” → HTT, THT, TTH
Event C: “Getting at least one H” → HTT, THT, TTH, THH, HTH, HHT, HHH
Here is a visual representation of events A, B and C.
From this visual representation of the events, it is easy to see that event B is totally included in event C, in the sense that every outcome in event B is also an outcome in event C. Also, note that event A stands apart from events B and C, in the sense that they have no outcome in common, or no overlap. At this point these are only noteworthy observations, but as you’ll discover later, they are very important ones.
Example
Staff Position
Consider Example 6, where we choose two candidates at random out of four (Ann, Beth, Jim and Dan). Recall that in this case the sample space is:
S = { (Ann, Beth), (Ann, Jim), (Ann, Dan), (Beth, Jim), (Beth, Dan), (Jim, Dan) }
In this example, we might be interested in the following events, each of which is a statement about the nature of the outcome that the random experiment will produce:
Event A: “Jim is chosen.”
Event B: “The two chosen are of the same gender.”
Again, each event corresponds to some collection of outcomes.
Once an event is defined, we can talk about the probability that it will occur. So, if we have defined an Event A, we can use the notation we previously mentioned to represent its probability, namely P(A).
The following figure summarizes the information in this section:
Equally Likely Outcomes
Learning Objective
In the Introduction to Probability (Module 7), we learned how the relative frequency approach can be used to estimate the probability of an event. While sometimes this is the only method that can be used to estimate probability (such as when figuring out the probabilities of the occurrence of different blood types among the population), this method requires a lot of time and effort, especially since in order to get reliable estimates we need to repeat the random experiment many times. We are now moving on to a different method, which can be applied in cases in which the random experiment produces outcomes that are all equally likely. We’ll start with a simple example to introduce the idea of the method, and then move on to more interesting examples.
Example
Rolling a Fair Die
When an ordinary fair die is rolled once, what is the probability that the number rolled is even? We’ll denote this event by E (for even), so we are interested in finding P(E). Let’s analyze this problem:
* The random experiment is rolling a fair die once.
* The sample space of all possible outcomes in this case this is S = {1, 2, 3, 4, 5, 6}.
* Since the die is fair, this means that all 6 possible outcomes are equally likely (each having a probability of 1/6 of occurring)
* We are interested in a particular type of outcome, which is represented by event E—getting an even number.
Since 3 out of the 6 equally likely outcomes make up the event E (the outcomes {2, 4, 6}),
the probability of event E is simply P(E) = 3/6.
Let’s Generalize
In the special situation where all the outcomes in S are equally likely, we can find the probability of any event A by dividing the number of outcomes in A by the number of outcomes in S:
The purpose of the next activity is to give you guided practice on how to find the probability of an event in situations in which all the possible outcomes are equally likely.
Did I get this?
A couple is planning to have 3 children. Assuming that having a boy and having a girl are equally likely, and that the gender of one child has no influence on (or, is independent of) the gender of another, what is the probability that the couple will have exactly 2 girls?
The “random experiment” in this case is having 3 children, as odd as that may sound in this context. The next and most important step is to determine what all of the possible outcomes are, and list them (i.e., list the sample space S). In this case, each outcome represents a possible combination of genders of 3 children (note that examples with the same number of boys and girls but a different birth order must be listed separately).
Here is a more interesting example:
Example
A certain college recently announced 2 job openings in its admissions office. From all the applicants, a search committee identified 5 candidates—2 men and 3 women—who seemed equally qualified. Priding itself on a long history as an equal opportunity employer, the college would like to continue that tradition and make the 2 appointments at random. The college’s legal department, though, has cautioned the personnel office that doing so may not be a good idea. If the 2 chosen happen to be of the same gender, the selection process will seem to be discriminatory, and the college may become embroiled in expensive litigation. What is the probability that the random selection will result in both chosen candidates having the same gender, and will thus appear to be discriminatory? We’ll denote this event by D (for discriminatory).
Let’s identify the 2 men and 3 women as M1, M2, F1, F2 and F3.
Our random experiment is choosing 2 out of these 5 candidates at random, and the sample space of all possible outcomes of this random experiment is therefore:
S = { (M1, M2), (M1, F1), (M1, F2), (M1, F3), (M2, F1), (M2, F2), (M2, F3), (F1, F2), (F1, F3), (F2, F3) }.
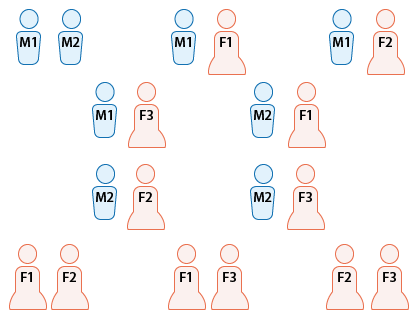
Note that because the order in which the selection is made does not matter, and because 2 candidates are being chosen and they are listed in S as pairs, once we’ve included (M1, M2) in S, we should not also include (M2, M1). Both represent the same outcome: M1 and M2 are the two that were chosen to get the jobs.
Thus S consists of 10 outcomes, all equally likely, since the selection of any 2 out of the 5 has been done at random.
We are interested in event D—that the selection process will appear to be discriminatory, or in other words that the two chosen will be of the same gender. Event D consists of 4 of the 10 possible outcomes:
D = { (M1,M2), (F1,F2), (F1,F3), (F2,F3) }
The probability that the selection will appear to be discriminatory is therefore: P(D) = 4/10
Comment
It should be noted that in this example it was still manageable to list all the possible outcomes, and then count the number of outcomes that are in event D. If we were to change the example slightly, and needed to choose 2 candidates out of, say, 10 (instead of 5), the number of possible outcomes would grow substantially (from 10 to 45) and listing all of those outcomes would be quite time-consuming and tiresome. Later in the probability section we will learn some simple counting methods that will allow us to figure out the number of possible outcomes without actually listing them.
Did I get this?
A flight has been overbooked; however, there are 2 seats available—one in business class and one in first class. The ground crew decides to upgrade 2 of the coach (regular class) passengers so that 2 more passengers will be able to get on the flight. The crew has identified 4 passengers, 2 males and 2 females, who are traveling by themselves and who have been loyal frequent fliers on the airline. They decide to choose 2 of those passengers at random for the upgrade. The first chosen will be upgraded to first class, and the second chosen will be upgraded to business class. We’ll denote the 2 males and 2 females (as before) with M1, M2, F1 and F2.
Comment
It is important to note that it is not always the case the all the outcomes of a random experiment are equally likely.
A common mistake among students who are exposed to probability for the first time is to assume that all the outcomes of a random experiment are equally likely when in fact they are not.
Here is an example.
Example
A fair coin is tossed repeatedly until the first ‘H’ is obtained but no more than three times. In this experiment there are four possible outcomes: Getting ‘H’ in the first toss, getting the first ‘H’ in the second toss, getting the first ‘H’ in the third toss, or tossing the coin three times without getting a ‘H’. The sample space in this case is therefore:
As mentioned above, a common mistake is to wrongly assume that the four outcomes are equally likely, each with probability ¼.
Note that the first outcomes ‘H’ has probability ½ (since it represents the outcome of tossing the fair coin once and getting ‘H’). If the first outcome has probability ½, it is clear that the outcomes cannot be equally likely since the sum of the probabilities of all outcomes must be 1.
To Summarize
In the special case when all the outcomes of a random experiment are equally likely, there is a simple way to calculate the probability of any event by counting how many of the outcomes satisfy or make up the event, and dividing it by the total number of outcomes in the sample space.
Remember, it is not always the case that the outcomes are equally likely, so make sure to check if they are before applying this method to calculate probabilities. In the next modules you’ll learn other methods which will help you compute probabilities more generally.
