3.4: Linear Regression Equation
Linear Regression: Summarizing the Pattern of the Data with a Line
So far we’ve used the scatterplot to describe the relationship between two quantitative variables, and in the special case of a linear relationship, we have supplemented the scatterplot with the correlation (r). The correlation, however, doesn’t fully characterize the linear relationship between two quantitative variables—it only measures the strength and direction. We often want to describe more precisely how one variable changes with the other (by “more precisely,” we mean more than just the direction), or predict the value of the response variable for a given value of the explanatory variable. In order to be able to do that, we need to summarize the linear relationship with a line that best fits the linear pattern of the data. In the remainder of this section, we will introduce a way to find such a line, learn how to interpret it, and use it (cautiously) to make predictions.
Again, let’s start with a motivating example:
Earlier, we examined the linear relationship between the age of a driver and the maximum distance at which a highway sign was legible, using both a scatterplot and the correlation coefficient. Suppose a government agency wanted to predict the maximum distance at which the sign would be legible for 60-year-old drivers, and thus make sure that the sign could be used safely and effectively.
How would we make this prediction?
The technique that specifies the dependence of the response variable on the explanatory variable is called regression. When that dependence is linear (which is the case in our examples in this section), the technique is called linear regression. Linear regression is therefore the technique of finding the line that best fits the pattern of the linear relationship (or in other words, the line that best describes how the response variable linearly depends on the explanatory variable).
To understand how such a line is chosen, consider the following very simplified version of the age-distance example (we left just 6 of the drivers on the scatterplot):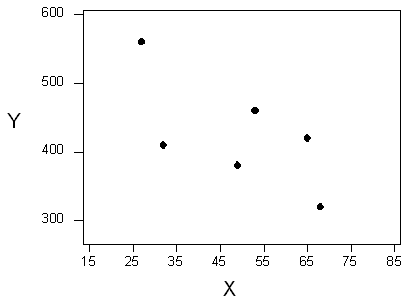
There are many lines that look like they would be good candidates to be the line that best fits the data:
It is doubtful that everyone would select the same line in the plot above. We need to agree on what we mean by “best fits the data”; in other words, we need to agree on a criterion by which we would select this line. We want the line we choose to be close to the data points. In other words, whatever criterion we choose, it had better somehow take into account the vertical deviations of the data points from the line, which are marked with blue arrows in the plot below:
The most commonly used criterion is called the least squares criterion. This criterion says: Among all the lines that look good on your data, choose the one that has the smallest sum of squared vertical deviations. Visually, each squared deviation is represented by the area of one of the squares in the plot below. Therefore, we are looking for the line that will have the smallest total yellow area. This line is called the least-squares regression line, and, as we’ll see, it fits the linear pattern of the data very well.
This line is called the least-squares regression line, and, as we’ll see, it fits the linear pattern of the data very well.
For the remainder of this lesson, you’ll need to feel comfortable with the algebra of a straight line. In particular you’ll need to be familiar with the slope and the intercept in the equation of a line, and their interpretation.
Like any other line, the equation of the least-squares regression line for summarizing the linear relationship between the response variable(Y) and the explanatory variable (X) has the form: Y = a + bX
All we need to do is calculate the intercept a, and the slope b, which is easily done if we know:
-
¯¯¯X—the mean of the explanatory variable’s values
-
SX—the standard deviation of the explanatory variable’s values
-
¯¯¯Y—the mean of the response variable’s values
-
SY—the standard deviation of the response variable’s values
-
r—the correlation coefficient
Given the five quantities above, the slope and intercept of the least squares regression line are found using the following formulas:
[latex]\mathcal{b}=\mathcal{r}\left(\frac{\mathcal{S}_\mathcal{y}}{\mathcal{S}_\mathcal{x}}\right)\\ \mathcal{a}=\bar{\mathcal{Y}}-\mathcal{b}\bar{\mathcal{X}}[/latex]
Comments
-
Note that since the formula for the intercept a depends on the value of the slope, b, you need to find b first.
-
The slope of the least squares regression line can be interpreted as the average change in the response variable when the explanatory variable increases by 1 unit.
Example
Age-Distance
Let’s revisit our age-distance example, and find the least-squares regression line. The following output will be helpful in getting the 5 values we need:

-
The slope of the line is [latex]\mathcal{b}=\left(-0.793\right)*\left(\frac{82.8}{21.78}\right)=-3[/latex]. This means that for every 1-unit increase of the explanatory variable, there is, on average, a 3-unit decrease in the response variable. The interpretation in context of the slope being -3 is, therefore: For every year a driver gets older, the maximum distance at which he/she can read a sign decreases, on average, by 3 feet.
-
The intercept of the line is a=423−(−3∗51)=576 and therefore the least-squares regression line for this example is
Distance = 576 + (−3 * Age)
Here is the regression line plotted on the scatterplot: As we can see, the regression line fits the linear pattern of the data quite well.
As we can see, the regression line fits the linear pattern of the data quite well.
Comment
As we mentioned before, hand-calculation is not the focus of this course. We wanted you to see one example in which the least squares regression line is calculated by hand, but in general we’ll let a statistics package do that for us.
Let’s go back now to our motivating example, in which we wanted to predict the maximum distance at which a sign is legible for a 60-year-old. Now that we have found the least squares regression line, this prediction becomes quite easy:
Practically, what the figure tells us is that in order to find the predicted legibility distance for a 60-year-old, we plug Age = 60 into the regression line equation, to find that:
| Predicted distance = 576 + (- 3 * 60) = 396 |
396 feet is our best prediction for the maximum distance at which a sign is legible for a 60-year-old.
Did I get this?
Background: A statistics department is interested in tracking the progress of its students from entry until graduation. As part of the study, the department tabulates the performance of 10 students in an introductory course and in an upper-level course required for graduation. The scatterplot below includes the least squares line (the line that best explains the upper-level course average based on the lower-level course average), and its equation:

Comment About Predictions
Suppose a government agency wanted to design a sign appropriate for an even wider range of drivers than were present in the original study. They want to predict the maximum distance at which the sign would be legible for a 90-year-old. Using the least squares regression line again as our summary of the linear dependence of the distances upon the drivers’ ages, the agency predicts that 90-year-old drivers can see the sign at no more than 576 + (- 3 * 90) = 306 feet:
(The green segment of the line is the region of ages beyond 82, the age of the oldest individual in the study.)
In General
Prediction for ranges of the explanatory variable that are not in the data is called extrapolation. Since there is no way of knowing whether a relationship holds beyond the range of the explanatory variable in the data, extrapolation is not reliable, and should be avoided. In our example, like most others, extrapolation can lead to very poor or illogical predictions.
Let’s Summarize
- A special case of the relationship between two quantitative variables is the linear relationship. In this case, a straight line simply and adequately summarizes the relationship.
- When the scatterplot displays a linear relationship, we supplement it with the correlation coefficient (r), which measures the strength and direction of a linear relationship between two quantitative variables. The correlation ranges between -1 and 1. Values near -1 indicate a strong negative linear relationship, values near 0 indicate a weak linear relationship, and values near 1 indicate a strong positive linear relationship.
- The correlation is only an appropriate numerical measure for linear relationships, and is sensitive to outliers. Therefore, the correlation should only be used as a supplement to a scatterplot (after we look at the data).
- The most commonly used criterion for finding a line that summarizes the pattern of a linear relationship is “least squares.” The least squares regression line has the smallest sum of squared vertical deviations of the data points from the line.
- The slope of the least squares regression line can be interpreted as the average change in the response variable when the explanatory variable increases by 1 unit.
- The least squares regression line predicts the value of the response variable for a given value of the explanatory variable. Extrapolation is prediction of values of the explanatory variable that fall outside the range of the data. Since there is no way of knowing whether a relationship holds beyond the range of the explanatory variable in the data, extrapolation is not reliable, and should be avoided.
Causation
So far we have discussed different ways in which data can be used to explore the relationship (or association) between two variables. To frame our discussion we followed the role-type classification table:
and we have now completed learning how to explore the relationship in cases C→Q, C→C, and Q→Q. (As noted before, case Q→C will not be discussed in this course.) When we explore the relationship between two variables, there is often a temptation to conclude from the observed relationship that changes in the explanatory variable cause changes in the response variable. In other words, you might be tempted to interpret the observed association as causation. The purpose of this part of the course is to convince you that this kind of interpretation is often wrong! The motto of this section is one of the most fundamental principles of this course:
| Principle |
|---|
|
Association does not imply causation! |
Example
Fire Damage
The scatterplot below illustrates how the number of firefighters sent to fires (X) is related to the amount of damage caused by fires (Y) in a certain city.
The scatterplot clearly displays a fairly strong (slightly curved) positive relationship between the two variables. Would it, then, be reasonable to conclude that sending more firefighters to a fire causes more damage, or that the city should send fewer firefighters to a fire, in order to decrease the amount of damage done by the fire? Of course not! So what is going on here?
There is a third variable in the background—the seriousness of the fire—that is responsible for the observed relationship. More serious fires require more firefighters, and also cause more damage.
The following figure will help you visualize this situation:
Here, the seriousness of the fire is a lurking variable. A lurking variable is a variable that is not among the explanatory or response variables in a study, but could substantially affect your interpretation of the relationship among those variables.
In particular, as in our example, the lurking variable might have an effect on both the explanatory and the response variables. This common effect creates the observed association between the explanatory and response variables, even though there is no causal link between them. This possibility, that there might be a lurking variable (which we might not be thinking about) that is responsible for the observed relationship leads to our principle:
| Principle |
|---|
|
Association does not imply causation! |
The next example will illustrate another way in which a lurking variable might interfere and prevent us from reaching any causal conclusions.
Example
SAT Test
For U.S. colleges and universities, a standard entrance examination is the SAT test. The side-by-side boxplots below provide evidence of a relationship between the student’s country of origin (the United States or another country) and the student’s SAT Math score.
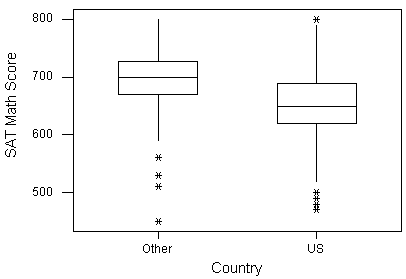
The distribution of international students’ scores is higher than that of U.S. students. The international students’ median score (about 700) exceeds the third quartile of U.S. students’ scores. Can we conclude that the country of origin is the cause of the difference in SAT Math scores, and that students in the United States are weaker at math than students in other countries?
No, not necessarily. While it might be true that U.S. students differ in math ability from other students—i.e. due to differences in educational systems—we can’t conclude that a student’s country of origin is the cause of the disparity. One important lurking variable that might explain the observed relationship is the educational level of the two populations taking the SAT Math test. In the United States, the SAT is a standard test, and therefore a broad cross-section of all U.S. students (in terms of educational level) take this test. Among all international students, on the other hand, only those who plan on coming to the U.S. to study, which is usually a more selected subgroup, take the test.
The following figure will help you visualize this explanation:

Here, the explanatory variable (X) may have a causal relationship with the response variable (Y), but the lurking variable might be a contributing factor as well, which makes it very hard to isolate the effect of the explanatory variable and prove that it has a causal link with the response variable. In this case, we say that the lurking variable is confounded with the explanatory variable, since their effects on the response variable cannot be distinguished from each other.
Note that in each of the above two examples, the lurking variable interacts differently with the variables studied. In example 1, the lurking variable has an effect on both the explanatory and the response variables, creating the illusion that there is a causal link between them. In example two, the lurking variable is confounded with the explanatory variable, making it hard to assess the isolated effect of the explanatory variable on the response variable.
The distinction between these two types of interactions is not as important as the fact that in either case, the observed association can be at least partially explained by the lurking variable. The most important message from these two examples is therefore: An observed association between two variables is not enough evidence that there is a causal relationship between them.
In other words …
| Principle |
|---|
|
Association does not imply causation! |
Did I get this?
So far, we have:
- discussed what lurking variables are,
- demonstrated different ways in which the lurking variables can interact with the two studied variables, and
- understood that the existence of a possible lurking variable is the main reason why we say that association does not imply causation.
As you recall, a lurking variable, by definition, is a variable that was not included in the study, but could have a substantial effect on our understanding of the relationship between the two studied variables.
What if we did include a lurking variable in our study? What kind of effect could that have on our understanding of the relationship? These are the questions we are going to discuss next.
Let’s start with an example:
Example
Hospital Death Rates
Background: A government study collected data on the death rates in nearly 6,000 hospitals in the United States. These results were then challenged by researchers, who said that the federal analyses failed to take into account the variation among hospitals in the severity of patients’ illnesses when they were hospitalized. As a result, said the researchers, some hospitals were treated unfairly in the findings, which named hospitals with higher-than-expected death rates. What the researchers meant is that when the federal government explored the relationship between the two variables—hospital and death rate—it also should have included in the study (or taken into account) the lurking variable—severity of illness.
We will use a simplified version of this study to illustrate the researchers’ claim, and see what the possible effect could be of including a lurking variable in a study. (Reference: Moore and McCabe (2003). Introduction to the Practice of Statistics.)
Consider the following two-way table, which summarizes the data about the status of patients who were admitted to two hospitals in a certain city (Hospital A and Hospital B). Note that since the purpose of the study is to examine whether there is a “hospital effect” on patients’ status, “Hospital is the explanatory variable, and “Patient’s Status” is the response variable.
When we supplement the two-way table with the conditional percents within each hospital:
we find that Hospital A has a higher death rate (3%) than Hospital B (2%). Should we jump to the conclusion that a sick patient admitted to Hospital A is 50% more likely to die than if he/she were admitted to Hospital B? Not so fast …
Maybe Hospital A gets most of the severe cases, and that explains why it has a higher death rate. In order to explore this, we need to include (or account for) the lurking variable “severity of illness” in our analysis. To do this, we go back to the two-way table and split it up to look separately at patents who are severely ill, and patients who are not.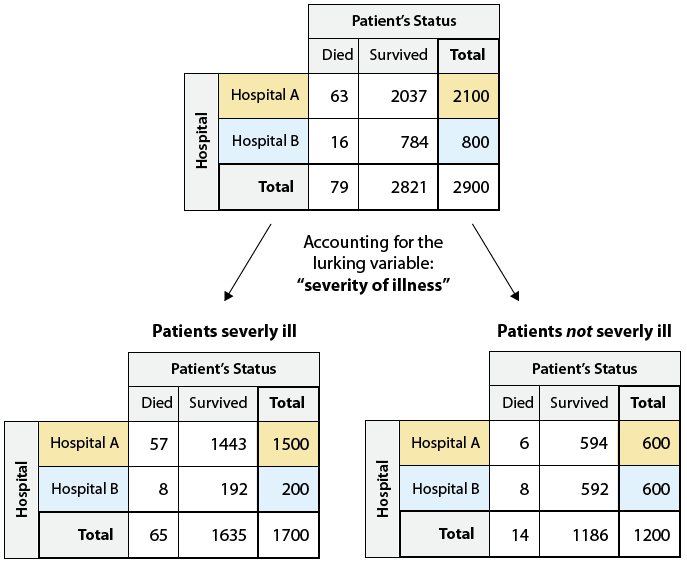
As we can see, Hospital A did admit many more severely ill patients than Hospital B (1,500 vs. 200). In fact, from the way the totals were split, we see that in Hospital A, severely ill patients were a much higher proportion of the patients—1,500 out of a total of 2,100 patients. In contrast, only 200 out of 800 patients at Hospital B were severely ill. To better see the effect of including the lurking variable, we need to supplement each of the two new two-way tables with its conditional percentages: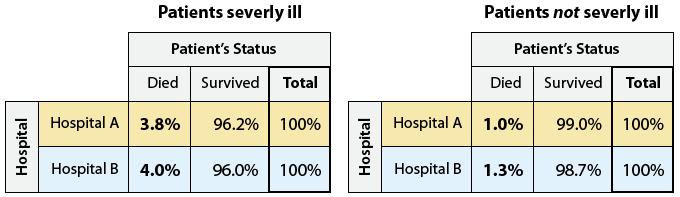
Note that despite our earlier finding that overall Hospital A has a higher death rate (3% vs. 2%), when we take into account the lurking variable, we find that actually it is Hospital B that has the higher death rate both among the severely ill patients (4% vs. 3.8%) and among the not severely ill patients (1.3% vs. 1%). Thus, we see that adding a lurking variable can change the direction of an association.
Whenever including a lurking variable causes us to rethink the direction of an association, this is called Simpson’s paradox.
The possibility that a lurking variable can have such a dramatic effect is another reason we must adhere to the principle:
| Principle |
|---|
|
Association does not imply causation! |
It is not always the case that including a lurking variable makes us rethink the direction of the association. In the next example we will see how including a lurking variable just helps us gain a deeper understanding of the observed relationship.
Example
College Entrance Exams
As discussed earlier, in the United States, the SAT is a widely used college entrance examination, required by the most prestigious schools. In some states, a different college entrance examination is prevalent, the ACT.
The last two examples showed us that including a lurking variable in our exploration may
- Lead us to rethink the direction of an association (as in the Hospital/Death Rate example).
- Help us to gain a deeper understanding of the relationship between variables (as in the SAT/ACT example)
Did I get this?
Let’s Summarize
- A lurking variable is a variable that was not included in your analysis, but that could substantially change your interpretation of the data if it were included.
- Because of the possibility of lurking variables, we adhere to the principle that association does not imply causation.
- Including a lurking variable in our exploration may:
- Help us to gain a deeper understanding of the relationship between variables.
- Lead us to rethink the direction of an association.
- Whenever including a lurking variable causes us to rethink the direction of an association, this is an instance of Simpson’s paradox.

