2.3: Measures of Spread

Introduction

So far we have learned about different ways to quantify the center of a distribution. A measure of center by itself is not enough, though, to describe a distribution. Consider the following two distributions of exam scores. Both distributions are centered at 70 (the median of both distributions is approximately 70), but the distributions are quite different. The first distribution has a much larger variability in scores compared to the second one.

Two dot plots of exam scores. The first plot has a median of approximately 70, but there are scores from below 50 to above 90. In the second dot plot, the median is once again about 70, but this time the range of scores is from about 60 to about 80.

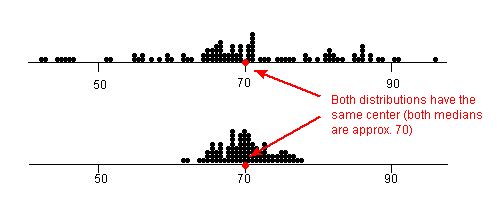
In order to describe the distribution, we therefore need to supplement the graphical display not only with a measure of center, but also with a measure of the variability (or spread) of the distribution.

In this section, we will discuss the three most commonly used measures of spread:

  • Range
  • Inter-quartile range (IQR)
  • Standard deviation

Like the different measures of center, these measures provide different ways to quantify the variability of the distribution.

Range

The range covered by the data is the most intuitive measure of variability. The range is exactly the distance between the smallest data point (min) and the largest one (Max).

  • Range = Max – min

Note: When we first looked at the histogram, and tried to get a first feel for the spread of the data, we were actually approximating the range, rather than calculating the exact range.

Example

Best Actress Oscar Winners

We will continue with the Best Actress Oscar winners example (To see the full dataset, click here.)

34 34 27 37 42 41 36 32 41 33 31 74 33 49 38 61 21 41 26 80 42 29 33 36 45 49 39 34 26 25 33 35 35 28 30 29 61 32 33 45 29 62 22 44

In this example:

  • min = 21 (Marlee Matlin for Children of a Lesser God, 1986)
  • Max = 80 (Jessica Tandy for Driving Miss Daisy, 1989)

The range covered by all the data is 80 – 21 = 59 years.

Inter-Quartile Range (IQR)

While the range quantifies the variability by looking at the range covered by ALL the data, the IQR measures the variability of a distribution by giving us the range covered by the MIDDLE 50% of the data.

The following picture illustrates this idea: (Think about the horizontal line as the data ranging from the min to the Max).

A horizontal line representing all of the data. The entire line represents the range of the data, and the leftmost point is the minimum data point. The rightmost point is the maximum data point. 25% of the range spanning the area between the leftmost point and 1/4 of the line from the leftmost point is labeled the Bottom 25% of the data. The area from the 1/4 point to the 3/4 point is labeled the middle 50% of the data. This is where the IQR is calculated. Indeed, the middle 50% represents half of the line. The rest of the line, the remaining 1/4 from the 3/4 point to the rightmost point, is the top 25% of the data.

Here is how the IQR is actually found:

  1. Arrange the data in increasing order, and find the median M. Recall that the median divides the data, so that 50% of the data points are below the median, and 50% of the data points are above the median.A line representing the range of the data. Once again, the leftmost point is the minimum, and the rightmost point is the maximum. At the middle is M, the median. All of the line to the left of M is the bottom 50% of the data, and all of the line to the right of M is the top 50% of the data.
  2. Find the median of the lower 50% of the data. This is called the first quartile of the distribution, and the point is denoted by Q1. Note from the picture that Q1 divides the lower 50% of the data into two halves, containing 25% of the data points in each half. Q1 is called the first quartile, since one quarter of the data points fall below it.The same line as the image above, except the bottom 50% has been split in half at the median of all of the data in the bottom 50%. This median is Q1. To the left of Q1 is 25% of the data. This is between the minimum point and Q1. On the other side of Q1 is another 25% of the data. This is from Q1 to M. Together these two 25% sections make up the bottom 50% of the data. To the right of M is the top 50% of the data, so in total, to the right of Q1 is 25% of the data and the top 50% of the data, for a total of 75% of the data.
  3. Repeat this again for the top 50% of the data. Find the median of the top 50% of the data. This point is called the third quartile of the distribution, and is denoted by Q3. Note from the picture that Q3 divides the top 50% of the data into two halves, with 25% of the data points in each. Q3 is called the third quartile, since three quarters of the data points fall below it.The same line as the image above, except the top 50% has been split in half at the median of all of the data in the top 50%. This median is Q3. To the left of Q3 is 25% of the data. This is between M and Q3. On the other side of Q3 is another 25% of the data. This is from Q3 to the maximum point. Together these two 25% sections make up the top 50% of the data. To the left of M is the top 50% of the data, so in total, to the left of Q3 is 25% of the data and the bottom 50% of the data, for a total of 75% of the data.
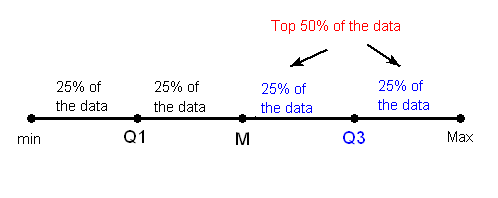
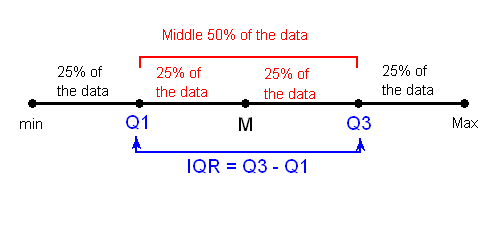
  4. The middle 50% of the data falls between Q1 and Q3, and therefore:

    IQR = Q3 – Q1

    A line representing the range of data. The leftmost point is the minimum point and the rightmost point is the maximum point. 25% of the line starting at the minimum point is the area to the left of Q1. To the right of Q1, going right another 25% of the line brings us to M. Going right another 25% brings us to Q3, and the last 25% brings us to the maximum point. The line segment between Q1 and Q3 is the middle 50% of the data, which is used for to calculate IQR = Q3-Q1

Comments

  1. The last picture shows that Q1, M, and Q3 divide the data into four quarters with 25% of the data points in each, where the median is essentially the second quartile. The use of IQR = Q3 – Q1 as a measure of spread is therefore particularly appropriate when the median M is used as a measure of center.

  2. We can define a bit more precisely what is considered the bottom or top 50% of the data. The bottom (top) 50% of the data is all the observations whose position in the ordered list is to the left (right) of the location of the overall median M. The following picture will visually illustrate this for the simple cases of n = 7 and n = 8.

    Two sets of dots. The first set of dots consists of 7 dots. These dots represent data points, and they are ordered so that the dots are in a line, from least to greatest. The 4th dot is the middle dot, so this is the median. The bottom 50% of the data are the 3 dots to the left of the 4th dot, and the top 50% of the data are the 3 dots to the right of the 4th dot. In the second set of dots, we have 8 dots, arranged from least to greatest. There is no middle dot, so the median M is the average of the 4th and 5th dots. The 4 dots from the 1st to 4th dot are the bottom 50% of the data, and the four dots from the 5th to 8th are the top 50% of the data.

    Note that when n is odd (as in n = 7 above), the median is not included in either the bottom or top half of the data; When n is even (as in n = 8 above), the data are naturally divided into two halves.

Example

Best Actress Oscar Winners

To find the IQR of the Best Actress Oscar winners distribution, it will be convenient to use the stemplot.

Stem plot of the Best Actress Oscar winners. The lower half of the step plot is the bottom half and the upper half is the top half. The stem plot is described in a stem|leaves format in row order. Note that the bottom half ends and the top half begins in the middle of a line (between two leaves). We begin with the bottom half: 2|12 2|56678999 3|012233333344 3|The top half: 3|4 3|5566789 4|1112244 4|99 5| 5| 6|112 6| 7|4 7| 8|0

Q1 is the median of the bottom half of the data. Since there are 22 observations in that half, Q1 is the mean of the 11th and 12th ranked observations in that half:

[latex]Q1=\frac{(30+31)}{2}=30.5[/latex]

Similarly, Q3 is the median of the top half of the data, and since there are 22 observations in that half, Q3 is the mean of the 11th and 12th ranked observations in that half:

[latex]Q3=\frac{(42+42)}{2}=42[/latex]

IQR = (42 −30.5 ) = 11.5

Note that in this example, the range covered by all the ages is 59 years, while the range covered by the middle 50% of the ages is only 11.5 years. While the whole dataset is spread over a range of 59 years, the middle 50% of the data is packed into only 11.5 years. Looking again at the histogram will illustrate this:

Histogram of the Best Actress Oscar Winners with the Range and IQR labeled. Recall that the histogram is skewed right. While the range encompasses the entire histogram, the IQR starts at x=30.5 and ends at x=42 , which is located within area of ages with higher frequencies on the histogram.

Comment

Software packages use different formulas to calculate the quartiles Q1 and Q3. This should not worry you, as long as you understand the idea behind these concepts. For example, here are the quartile values provided by three different software packages for the age of best actress Oscar winners:

R:

A snippet of output from R. It shows that: Min=21.00, Q1=32.50, Median=35, Q3=41.25, Max=80.00 .

Minitab:

A snippet of output from Minitab. It shows that N=32, Mean=38.53, Median=35.00, TrMean=36.89, StDev=12.95, SE Mean=2.29, Minimum=21.00, Maximum=80.00, Q1=31.50, Q2=41.75 .

Excel:

Four cells from a Excel spreadsheet showing that Q1=32.5 and Q3=41.25 .

Note that Q1 and Q3 as reported by the various software packages differ from each other and are also slightly different from the ones we found here. There are different acceptable ways to find the median and the quartiles. These can give different results occasionally, especially for datasets where n (the number of observations) is fairly small. As long as you know what the numbers mean, and how to interpret them in context, it doesn’t really matter much what method you use to find them, since the differences are really negligible.

Using the IQR to Detect Outliers

So far we have quantified the idea of center, and we are in the middle of the discussion about measuring spread, but we haven’t really talked about a method or rule that will help us classify extreme observations as outliers. The IQR is used as the basis for a rule of thumb for identifying outliers.

The 1.5(IQR) Criterion for Outliers

An observation is considered a suspected outlier if it is:

  • below Q1 – 1.5(IQR) or
  • above Q3 + 1.5(IQR)

The following picture illustrates this rule:

A line representing all of the data. The data is ordered so that the minimum point is the leftmost on the line and the maximum point is the rightmost. At the center of the line is M, the median, and to the left of M is Q1. Even farther to the left of Q1 is Q1-1.5(IQR). Points farther left than this are suspected outliers. To the right of M is Q3, and farther to the right is Q3+1.5(IQR). Points even farther than this are also suspected outliers.

Example

Best Actress Oscar Winners

We will continue with the Best Actress Oscar winners example (To see the data, click here).

34 34 27 37 42 41 36 32 41 33 31 74 33 49 38 61 21 41 26 80 42 29 33 36 45 49 39 34 26 25 33 35 35 28 30 29 61 32 33 45 29 62 22 44

 

Recall that when we first looked at the histogram of ages of Best Actress Oscar winners, there were 5 observations that looked like possible outliers:

A histogram of the Oscar winners in which for x=62 the frequency is 3 and for x=74 and x=80, the frequency is 1. Those points are thought to be possible outliers.

We can now use the 1.5(IQR) criterion to check whether the 5 observations should indeed be classified as outliers:

  • For this example we found that Q1=30.5andQ3=42.5⇒IQR=11.5
  • Q1−1.5(IQR)=30.5−(1.5)(11.5)=13.25
  • Q3+1.5(IQR)=42.5+(1.5)(11.5)=59.25

The 1.5(IQR) criterion tells us that any observation that is below 13.25 or above 59.25 is considered a suspected outlier.

We therefore conclude that the observations 61, 61, 62, 74 and 80 should be flagged as suspected outliers in the distribution of ages. Note that since the smallest observation is 21, there are no suspected low outliers in this distribution.

Did I get this?

Understanding Outliers

We just practiced one way to ‘flag’ possible outliers. Why is it important to identify possible outliers, and how should they be dealt with? The answers to these questions depend on the reasons for the outlying values. Here are several possibilities:

  1. Even though it is an extreme value, if an outlier can be understood to have been produced by essentially the same sort of physical or biological process as the rest of the data, and if such extreme values are expected to eventually occur again, then such an outlier indicates something important and interesting about the process you’re investigating, and it should be kept in the data.

  2. If an outlier can be explained to have been produced under fundamentally different conditions from the rest of the data (or by a fundamentally different process), such an outlier can be removed from the data if your goal is to investigate only the process that produced the rest of the data.

  3. An outlier might indicate a mistake in the data (like a typo, or a measuring error), in which case it should be corrected if possible or else removed from the data before calculating summary statistics or making inferences from the data (and the reason for the mistake should be investigated).

Here are examples of each of these types of outliers:

  1. The following histogram displays the magnitude of 460 earthquakes in California, occurring in the year 2000, between August 28 and September 9:

    A histogram titled "California Earthquakes, Aug 28,2000 - Sep 9,2000". The histogram is skewed-right. Frequency on the Y-axis ranges from 0 to 90, and on the X-axis is Magnitude in Richter units, from 0 to 5.4 . As we go from left to right across the X-axis, the frequency increases to the mode at x=1.2, y=90, then it decreases to 0 after x=3.6. However, beyond 4.8, we see a small bar representing a frequency of 1.

    Identifying the outlier:

    On the very far right edge of the display (beyond 4.8), we see a low bar; this represents one earthquake (because the bar has height of 1) that was much more severe than the others in the data.

    Understanding the outlier:

    In this case, the outlier represents a much stronger earthquake, which is relatively rarer than the smaller quakes that happen more frequently in California.

    How to handle the outlier:

    For many purposes, the relatively severe quakes represented by the outlier might be the most important (because, for instance, that sort of quake has the potential to do more damage to people and infrastructure). The smaller-magnitude quakes might not do any damage, or even be felt at all. So, for many purposes it could be important to keep this outlier in the data.

  2. The following histogram displays the monthly percent return on the stock of Phillip Morris (a large tobacco company) from July 1990 to May 1997:A histogram titled "Phillip Morris Monthly Stock Return, July 1990 - May 1997. On the Y-axis is Frequency, from 0 to 30. On the X-axis is Monthy Stock Return in percent. It ranges from -30 to 20. The histogram is skewed-left. At the very left, between at the interval x=(-30, -25), a bar indicating frequency of 1 appears. Then, we see no bar until x=-15, where there is a bar of frequency 5. As we continue moving right along the x-axis, frequency increases to the mode of 30 at the interval x=(0,5), and then decreases, until reaching a frequency of 5 at the interval x=(15,20).

    Identifying the outlier:

    On the display, we see a low bar far to the left of the others; this represents one month’s return (because the bar has height of 1), where the value of Phillip Morris stock was unusually low.

    Understanding the outlier:

    The explanation for this particular outlier is that, in the early 1990s, there were highly-publicized federal hearings being conducted regarding the addictiveness of smoking, and there was growing public sentiment against the tobacco companies. The unusually low monthly value in the Phillip Morris dataset was due to public pressure against smoking, which negatively affected the company’s stock for that particular month.

    How to handle the outlier:

    In this case, the outlier was due to unusual conditions during one particular month that aren’t expected to be repeated, and that were fundamentally different from the conditions that produced the values in all the other months. So in this case, it would be reasonable to remove the outlier, if we wanted to characterize the ‘typical’ monthly return on Phillip Morris stock.

  3. When archaeologists dig up objects such as pieces of ancient pottery, chemical analysis can be performed on the artifacts. The chemical content of pottery can vary depending on the type of clay as well as the particular manufacturing technique. The following histogram displays the results of one such actual chemical analysis, performed on 48 ancient Roman pottery artifacts from archaeological sites in Britain:

    A histogram titled "Manganous Oxide Content in a sample of Ancient Roman Pottery". The X-axis is labeled "number of pottery shards", and ranges from 0 to 20. The Y-axis is labeled "manganous oxide [MnO] content" and ranges from 0.0 to 0.4 . The histogram is skewed-right. Here are the bars: x=0.0,y=10; x=0.05,y=13; x=0.1,y=18; x=0.15,y=5; x=0.20,y=1; x=0.4,y=1. Note that there are no shards for x=0.25 to x=0.35

    Identifying the outlier:

    On the display, we see a low bar far to the right of the others; this represents one piece of pottery (because the bar has a height of 1), which has a suspiciously high manganous oxide value.

    Understanding the outlier:

    Based on comparison with other pieces of pottery found at the same site, and based on expert understanding of the typical content of this particular compound, it was concluded that the unusually high value was most likely a typo that was made when the data were published in the original 1980 paper (it was typed as “.394” but it was probably meant to be “.094”).

    How to handle the outlier:

    In this case, since the outlier was judged to be a mistake, it should be removed from the data before further analysis. In fact, removing the outlier is useful not only because it’s a mistake, but also because doing so reveals important structure that was otherwise hidden. This feature is evident on the next display:

    A histogram titled " Histogram without the outlier" The Y-axis is labeled "number of pottery shards", and it ranges from 0 to 12. The X-axis is labeled "manganous oxide [MnO] content" and ranges from 0.00 to about 0.18. Going from left to right along the X-axis reveals that at x=0, there is a frequency of 10. Then, there are no bars until x=0.4 . From here the bars increase in height until x=0.08, where the frequency is 12. Then the bars begin to decrease.

    When the outlier is removed, the display is re-scaled so that now we can see the set of 10 pottery pieces that had almost no manganous oxide. These 10 pieces might have been made with a different potting technique, so identifying them as different from the rest is historically useful. This feature was only evident after the outlier was removed.

Let’s Summarize

  • The range covered by the data is the most intuitive measure of spread and is exactly the distance between the smallest data point (min) and the largest one (Max).

  • Another measure of spread is the inter-quartile range (IQR), which is the range covered by the middle 50% of the data.

  • IQR = Q3 – Q1, the difference between the third and first quartiles. The first quartile (Q1) is the value such that one quarter (25%) of the data points fall below it, or the median of the bottom half of the data. The third quartile is the value such that three quarters (75%) of the data points fall below it, or the median of the top half of the data.

  • The IQR should be used as a measure of spread of a distribution only when the median is used as a measure of center.

  • The IQR can be used to detect outliers using the 1.5(IQR) criterion. Outliers are observations that fall below Q1 – 1.5(IQR) or above Q3 + 1.5(IQR).

Introduction

Before we move on to the third measure of spread (standard deviation), we’ll summarize what we’ve learned so far about measuring spread and use it to introduce another graphical display of the distribution of a quantitative variable, the boxplot.

The Five Number Summary

So far, in our discussion about measures of spread, the key players were:

  • the extremes (min and Max), which provide the range covered by all the data; and

  • the quartiles (Q1, M and Q3), which together provide the IQR, the range covered by the middle 50% of the data.

The combination of all five numbers (min, Q1, M, Q3, Max) is called the five number summary, and provides a quick numerical description of both the center and spread of a distribution.

Example

Best Actress Oscar Winners

We will continue with the Best Actress Oscar winners example (To see the data, click here.)

34 34 27 37 42 41 36 32 41 33 31 74 33 49 38 61 21 41 26 80 42 29 33 36 45 49 39 34 26 25 33 35 35 28 30 29 61 32 33 45 29 62 22 44 The five number summary of the age of Best Actress Oscar winners (1970-2013) is:

Min: 21

Q1: 30.5

M: 34.5

Q3: 42

Max: 80

Now that you understand what each of the five numbers means, you can appreciate how much information about the distribution is packed into the five-number summary. All this information can also be represented visually by using the boxplot.

The Boxplot

The boxplot graphically represents the distribution of a quantitative variable by visually displaying the five-number summary and any observation that was classified as a suspected outlier using the 1.5(IQR) criterion.

There are several ways to plot the whiskers on a boxplot. One convention is to plot whiskers down to the minimum and up to the maximum value. We use the 1.5(IQR criterion), also known as the Tukey method for plotting whiskers. First, calculate the IQR, the difference between the 75th and 25th percentiles (or Q3 – Q1). Multiply the IQR by 1.5. Add this value to the 75th percentile. If the value is greater than (or equal to) the maximum value in the dataset, draw the upper whisker to the maximum value. Otherwise, stop the whisker at the largest value that is less than 75th percentile + 1.5 * IQR. Plot any values that are greater than this as individual points that are outliers. Similarly, subtract 1.5 * IQR from the 25th percentile. If this value is smaller than the minimum value in the dataset, draw the lower whisker to the minimum value. Otherwise, stop the whisker at the lowest value that is greater than 25th percentile – 1.5 * IQR. Plot any values that are smaller than this as individual points that are outliers.

Using the Best Actress dataset, here is how we determine where to draw the whiskers:

  • Q3 = 42

  • Q1 = 30.5

  • IQR: 42 – 30.5 = 11.5

  • 1.5 * IQR = 1.5 * 11.5 = 17.25

  • Q3 + 1.5 * IQR = 42 + 17.25 = 59.25

The largest observation that is less than or equal to 59.25 is 49 so we draw the upper whisker up to 49. All points above 49 are considered outliers (61, 61, 62, 74, 80).

Q1 – 1.5 * IQR = 30.5 – 17.25 = 13.25

The smallest observation that is greater than or equal to 13.5 is 21 so we draw the lower whisker down to 21, which is also the minimum. There are no outliers.

Here is how a boxplot is constructed: (this is for the “Best Actress” dataset—to see the dataset, click here.)

 

GeoGebra Group offers a simulation activity where you can practice calculating the median, Q1, Q3, IQR, and outliers and drawing a boxplot. Note that you can edit the data in the chart to see different results.

To view this interactive simulation in a separate window click here.

https://www.geogebra.org/m/KhKTscBY

CC BY-SA 3.0 by GeoGebra Group

Did I get this?

boxplot graph with question mark next to the top box

 

boxplot graph with question mark next to the top line

 

boxplot graph with question mark next to an star above the top line

 

boxplot graph with question mark next to the bottom line

 

boxplot graph with question mark next to the bottom box

 

boxplot graph with question mark next to the middle line

 

boxplot graph with question mark next to red arrow going from bottom line to top star

 

boxplot graph with question mark next to arrow marking the height of both boxes

GeoGebra Group offers a simulation activity where you can practice calculating the median, Q1, Q3, IQR, and outliers and drawing a boxplot. Note that you can edit the data in the chart to see different results.

To view this interactive simulation in a separate window click here.

CC BY-SA 3.0 by GeoGebra Group

Did I get this?

The boxplot below displays ratings for TV shows during sweeps week:

boxplot graph for tv show ratings

Side-By-Side (Comparative) Boxplots

As we learned in the beginning of this module, the distribution of a quantitative variable is best represented graphically by a histogram. Boxplots are most useful when presented side-by-side for comparing and contrasting distributions from two or more groups.

Example

Best Actor/Actress Oscar Winners

So far we have examined the age distributions of Oscar winners for males and females separately.

It will be interesting to compare the age distributions of actors and actresses who won best acting Oscars. To do that we will look at side-by-side boxplots of the age distributions by gender. Recall also that we found the five-number summary and means for both distributions. For the Best Actress dataset, we did the calculations by hand. For the Best Actor dataset, we used statistical software, and here are the results we got:

  • Actors: min = 31, Q1 = 38, M = 43.5, Q3 = 50.5, Max = 76

  • Actresses: min = 21, Q1 = 30.5, M = 34.5, Q3 = 42, Max = 80

Based on the graph and numerical measures, we can make the following comparison between the two distributions:

Center: The graph reveals that the age distribution of the males is higher than the females’ age distribution. This is supported by the numerical measures. The median age for females (34.5) is lower than for the males (43.5). Actually, it should be noted that even the third quartile of the females’ distribution (42) is lower than the median age for males. We therefore conclude that in general, actresses win the Best Actress Oscar at a younger age than actors do.

Spread: Judging by the range of the data, there is much more variability in the females’ distribution (range = 59) than there is in the males’ distribution (range = 47). On the other hand, if we look at the IQR, which measures the variability only among the middle 50% of the distribution, we see slightly more spread in the ages of males (IQR = 12.5) than females (IQR = 11.5). We conclude that among all the winners, the actors’ ages are more alike than the actresses’ ages. However, the middle 50% of the age distribution of actresses is more homogeneous than the actors’ age distribution.

Outliers: We see that we have outliers in both distributions. There is only one high outlier in the actors’ distribution (76, Henry Fonda, On Golden Pond), compared with three high outliers in the actresses’ distribution.

Example

Temperature of Pittsburgh vs. San Francisco

In order to compare the average high temperatures of Pittsburgh to those in San Francisco we will look at the following side-by-side boxplots, and supplement the graph with the descriptive statistics of each of the two distributions.

A box plot titled "Average High Temperature: San Francisco vs. Pittsburgh". The vertical axis is in units of Temperature (F), and it goes from 30-80. There are two box plots, one for Pittsburgh and one for San Francisco.

Statistic

San Francisco

Pittsburgh

min

56.3

33.7

Q1

60.2

41.2

Median

62.7

61.4

Q3

65.35

77.75

Max

68.7

82.6

When looking at the graph, the similarities and differences between the two distributions are striking. Both distributions have roughly the same center (medians are 61.4 for Pitt, and 62.7 for San Francisco). However, the temperatures in Pittsburgh have a much larger variability than the temperatures in San Francisco (Range: 49 vs. 12. IQR: 36.5 vs. 5).

The practical interpretation of the results we got is that the weather in San Francisco is much more consistent than the weather in Pittsburgh, which varies a lot during the year. Also, because the temperatures in San Francisco vary so little during the year, knowing that the median temperature is around 63 is actually very informative. On the other hand, knowing that the median temperature in Pittsburgh is around 61 is practically useless, since temperatures vary so much during the year, and can get much warmer or much colder.

Note that this example provides more intuition about variability by interpreting small variability as consistency, and large variability as lack of consistency. Also, through this example we learned that the center of the distribution is more meaningful as a typical value for the distribution when there is little variability (or, as statisticians say, little “noise”) around it. When there is large variability, the center loses its practical meaning as a typical value.

Let’s Summarize

  • The five-number summary of a distribution consists of the median (M), the two quartiles (Q1, Q3) and the extremes (min, Max).

  • The five-number summary provides a complete numerical description of a distribution. The median describes the center, and the extremes (which give the range) and the quartiles (which give the IQR) describe the spread.

  • The boxplot graphically represents the distribution of a quantitative variable by visually displaying the five number summary and any observation that was classified as a suspected outlier using the 1.5 (IQR) criterion.

  • Boxplots are most useful when presented side-by-side to compare and contrast distributions from two or more groups.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intro to Statistics MAT1260 by SBCCOE is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book