10.2: Inference for Two Independent Means

Colorado Online

10.2: Inference for Two Independent Means

Learning Objectives

In a given context, carry out the inferential method for comparing groups and draw the appropriate conclusions.
Specify the null and alternative hypotheses for comparing groups.

Comparing Two Means—Two Independent Samples (The Two-Sample t-Test)

Overview

As we mentioned in the summary of the introduction to Case C→Q, the first case that we will deal with is comparing two means when the two samples are independent:

Sub-Population 1 has a Y Mean of μ_1, and Sub-Population 2 has a Y Mean of μ_2. From Sub-population 1 we take an SRS of size n_1, and from Sub-population 2 we take an SRS of size n_2. Both of these samples are independent.

Recall that here we are interested in the effect of a two-valued (k = 2) categorical variable (X) on a quantitative response (Y). Samples are drawn independently from the two sub-populations (defined by the two categories of X), and we need to evaluate whether or not the data provide enough evidence for us to believe that the two sub-population means are different.

In other words, our goal is to test whether the means μ₁ and μ₂ (which are the means of the variable of interest in the two sub-populations) are equal or not, and in order to do that we have two samples, one from each sub-population, which were chosen independently of each other. As the title of this part suggests, the test that we will learn here is commonly known as the two-sample t-test. As the name suggests, this is a t-test, which as we know means that the p-values for this test are calculated under some t distribution. Here is how this part is organized.

We first introduce our leading example, and then go in detail through the four steps of the two-sample t-test, illustrating each step using our example.

Note…Up until now, we have been dividing our population into sub-populations, then sampling from these sub-populations.

From now on, instead of calling them sub-populations, we will usually call the groups we wish to compare population 1, population 2, and so on. These two descriptions of the groups we are comparing can be used interchangeably.

Example

What is more important to you — personality or looks?

This question was asked of a random sample of 239 college students, who were to answer on a scale of 1 to 25. An answer of 1 means personality has maximum importance and looks no importance at all, whereas an answer of 25 means looks have maximum importance and personality no importance at all. The purpose of this survey was to examine whether males and females differ with respect to the importance of looks vs. personality.

To open Excel with the data in the worksheet, right-click here to download the file to your computer. Then find the downloaded file and double-click it to open it in Excel. When Excel opens, you may have to enable editing.

Note that the data have the following format:

Score (Y)	Gender (X)
15	Male
13	Female
10	Female
12	Male
14	Female
14	Male
6	Male
17	Male
etc.

The format of the data reminds us that we are essentially examining the relationship between the two-valued categorical variable, gender, and the quantitative response, score. The two values of the categorical explanatory variable define the two populations that we are comparing — males and females. The comparison is with respect to the response variable score. Here is a figure that summarizes the example:

We have two populations, Females and Males. This is our Gender (X) Variable. For each of these populations, there is a Score (Y) mean, μ_1 for Females and μ_2 for Males. For the Female population we generate an SRS of size 150. For Males, we generate a SRS of size 85.

Comments:

Note that this figure emphasizes how the fact that our explanatory is a two-valued categorical variable means that in practice we are comparing two populations (defined by these two values) with respect to our response Y.
Note that even though the problem description just says that we had 239 students, the figure tells us that there were 85 males in the sample, and 150 females.
Following up on comment 2, note that 85 + 150 = 235 and not 239. In these data (which are real) there are four “missing observations”—4 students for which we do not have the value of the response variable, “importance.” This could be due to a number of reasons, such as recording error or nonresponse. The bottom line is that even though data were collected from 239 students, effectively we have data from only 235. (Recommended: Go through the data file and note that there are 4 cases of missing observations: students 34, 138, 179, and 183).

The Two-Sample t-Test

Here again is the general situation which requires us to use the two-sample t-test:

Sub-Population 1 has a Y Mean of μ_1, and Sub-Population 2 has a Y Mean of μ_2. From Sub-population 1 we take an SRS of size n_1, and from Sub-population 2 we take an SRS of size n_2. Both of these samples are independent.

Our goal is to compare the means μ₁ and μ₂ based on the two independent samples.

Step 1: Stating the Hypotheses

The hypotheses represent our goal, comparing the means: μ₁ and μ₂ .

The null hypothesis has the form:
- $H_{o} : μ_{1} - μ_{2} = 0$ (which is the same as $H_{o} : μ_{1} = μ_{2}$ )
The alternative hypothesis takes one of the following three forms (depending on the context):
- $H_{a} : μ_{1} - μ_{2} < 0$ (which is the same as $H_{a} : μ_{1} < μ_{2}$ ) (one-sided)
- $H_{a} : μ_{1} - μ_{2} > 0$ (which is the same as $H_{a} : μ_{1} > μ_{2}$ ) (one-sided)
- $H_{a} : μ_{1} - μ_{2} \neq 0$ (which is the same as $H_{a} : μ_{1} \neq μ_{2}$ ) (two-sided)

Note that the null hypothesis claims that there is no difference between the means, which can either represented as the difference is 0 (no difference), or as its (algebraically and conceptually) equivalent, $μ_{1} = μ_{2}$ (the means are equal). Either way, conceptually, H_o claims that there is no relationship between the two relevant variables.

The first way of writing the hypotheses (using a difference between the means) will be easier to use when (in the future) we look for a difference that is not 0.

Each one of the three alternatives claims that there is a difference between the means. The two one-sided alternatives specify the nature of the difference; either negative, indicating that μ₁ is smaller than μ₂, or positive, indicating that μ₁ is larger than μ₂. The two-sided alternative, as usual, is more general and simply claims that a difference exists. As before, it should be clear from the context of the problem which of the three alternatives is appropriate.

Comment

Note that our parameter of interest in this case (the parameter about which we are making an inference) is the difference between the means $μ_{1} - μ_{2}$ , and that the null value is 0.

Example

Recall that the purpose of this survey was to examine whether the opinions of females and males differ with respect to the importance of looks vs. personality. The hypotheses in this case are therefore:

H_0: μ_1 - μ_2 = 0, H_a: μ_1 - μ_2 ≠ 0

where μ₁ represents the mean importance for females and μ₂ represents the mean importance for males.

It is important to understand that conceptually, the two hypotheses claim:

H_o: Score (of looks vs. personality) is not related to gender

H_a: Score (of looks vs. personality) is related to gender

Did I get this?

In order to check the claim that the pregnancy length of women who smoke during pregnancy is shorter, on average, than the pregnancy length of women who do not smoke, a random sample of 35 pregnant women who smoke and a random sample of 35 pregnant women who do not smoke were chosen and their pregnancy lengths were recorded. Here is a figure of this example:

Note that “mu” stands for the Greek letter μ, the population mean—mu1 stands for the mean of population 1 and mu2 stands for the mean of population 2.

Step 2: Check Conditions, and Summarize the Data Using a Test Statistic

The two-sample t-test can be safely used as long as the following conditions are met:

The two samples are indeed independent.
We are in one of the following two scenarios:
1. Both populations are normal, or more specifically, the distribution of the response Y in both populations is normal, and both samples are random (or at least can be considered as such). In practice, checking normality in the populations is done by looking at each of the samples using a histogram and checking whether there are any signs that the populations are not normal. Such signs could be extreme skewness and/or extreme outliers.
2. The populations are known or discovered not to be normal, but the sample size of each of the random samples is large enough (we can use the rule of thumb that > 30 is considered large enough).

Assuming that we can safely use the two-sample t-test, we need to summarize the data, and in particular, calculate our data summary—the test statistic.

The two-sample t-test statistic is:

[latex]\mathcal{t}=\frac{\bar{\mathcal{y}_1}-\bar{\mathcal{y}_2}-0}{\sqrt{\frac{\mathcal{s}_1^2}{\mathcal{n}_1}+\frac{\mathcal{s}_2^2}{\mathcal{n}_2}}}[/latex]

Where:

$¯ ¯ ¯ {y1}, ¯ ¯ ¯ {y2}$ are the sample means of the samples from population 1 and population 2 respectively.

${s1}, {s2}$ are the sample standard deviations of the samples from population 1 and population 2 respectively.

${n1}, {n2}$ are the sample sizes of the two samples.

Comment

Let’s see why this test statistic makes sense, bearing in mind that our inference is about $μ_{1} - μ_{2}$ .

$¯ ¯ ¯ y_{1}$ estimates μ₁ and $¯ ¯ ¯ y_{2}$ estimates μ₂, and therefore $¯ ¯ ¯ y_{1} - ¯ ¯ ¯ y_{2}$ is what the data tell me about (or, how the data estimate)

$μ_{1} - μ_{2}$ .
0 is the “null value” — what the null hypothesis, H_o, claims that $μ_{1} - μ_{2}$ is.
The denominator [latex]\sqrt{\frac{\mathcal{s}_1^2}{\mathcal{n}_1}+\frac{\mathcal{s}_2^2}{\mathcal{n}_2}}[/latex] is the standard error of $¯ ¯ ¯ y_{1} - ¯ ¯ ¯ y_{2}$ . (We will not go into the details of why this is true.)

We therefore see that our test statistic, like the previous test statistics we encountered, has the structure:

[latex]\frac{sample\ estimate-null\ value}{standard\ error}[/latex]

and therefore, like the previous test statistics, measures (in standard errors) the difference between what the data tell us about the parameter of interest $μ_{1} - μ_{2}$ (sample estimate) and what the null hypothesis claims the value of the parameter is (null value).

Example

Let’s first check whether the conditions that allow us to safely use the two-sample t-test are met.

Here, 239 students were chosen and were naturally divided into a sample of females and a sample of males. Since the students were chosen at random, the sample of females is independent of the sample of males.
Here we are in the second scenario — the sample sizes (150 and 85), are definitely large enough, and so we can proceed regardless of whether the populations are normal or not.

In order to avoid tedious calculations, we will lift the test statistic from the output. The StatCrunch output (edited) is shown below:

As you can see we highlighted the “ingredients” needed to calculate the test statistic, as well as the test statistic itself. Just for this first example, let’s make sure that we understand what these ingredients are and how to use them to find the test statistic.

Learn by Doing

And when we put it all together we get that indeed,

[latex]\mathcal{t}=\frac{\bar{\mathcal{y}_1}-\bar{\mathcal{y}_2}-0}{\sqrt{\frac{\mathcal{s}_1^2}{\mathcal{n}_1}+\frac{\mathcal{s}_2^2}{\mathcal{n}_2}}}=\ \frac{10.73-13.33}{\sqrt{\frac{{4.25}^2}{150}+\frac{{4.02}^2}{85}}}=-4.66[/latex]

The test statistic tells us what the data tell us about $μ_{1} - μ_{2}$ . In this case that difference (10.73 – 13.33) is 4.66 standard errors below what the null hypothesis claims this difference to be (0). 4.66 standard errors is quite a lot and probably indicates that the data provide evidence against H_o.

We have completed step 2 and are ready to proceed to step 3, finding the p-value of the test.

Step 3: Finding the p-value of the test

Since our test is called the two-sample t test ,we know that the p-values are calculated under a t distribution. Indeed, it turns out that the null distribution of our test statistic is approximately t. Figuring out which one of the t distributions (in other words, how many degrees of freedom this t distribution has) is quite involved and will not be discussed here. Instead, we use a statistics package to find that the p-value in this case is 0.

Example

Here, again is the relevant output for our example:

According to the output the p-value of this test is less than 0.0001. How do we interpret this?

A p-value which is practically 0 means that it would be almost impossible to get data like that observed (or even more extreme) had the null hypothesis been true.

More specifically to our example, if there were no differences between females and males with respect to whether they value looks vs. personality, it would be almost impossible (probability approximately 0) to get data where the difference between the sample means of females and males is -2.596 (that difference is 10.733 – 13.329 = -2.596) or higher.

Comment: Note that the output tells us that $¯ ¯ ¯ y_{1} - ¯ ¯ ¯ y_{2}$ is approximately -2.6. But more importantly, we want to know if this difference is significant. To answer this, we use the fact that this difference is 4.66 standard errors below the null value.

Step 4: Conclusion in context

As usual a small p-value provides evidence against H_o. In our case our p-value is practically 0 (which smaller than any level of significance that we will choose). The data therefore provide very strong evidence against H_o so we reject it and conclude that the mean Importance score (of looks vs personality) of males differs from that of females. In other words, males and females differ with respect to how they value looks vs. personality.

Comments

You might ask yourself: “Where do we use the test statistic?”

It is true that for all practical purposes all we have to do is check that the conditions which allow us to use the two-sample t-test are met, lift the p-value from the output, and draw our conclusions accordingly.

However, we feel that it is important to mention the test statistic for two reasons:

The test statistic is what’s behind the scenes; based on its null distribution and its value, the p-value is calculated.
Apart from being the key for calculating the p-value, the test statistic is also itself a measure of the evidence stored in the data against H_o. As we mentioned, it measures (in standard errors) how different our data is from what is claimed in the null hypothesis.

Let’s look at another example, and then you’ll do one yourself.

Example

According to the National Health And Nutrition Examination Survey (NHANES) sponsored by the U.S. government, a random sample of 712 males between 20 and 29 years of age and a random sample of 1,001 males over the age of 75 were chosen, and the weight of each of the males was recorded (in kg). Here is a summary of the results (source: http://www.cdc.gov/nchs/data/ad/ad347.pdf):

For males 20-29 years old, n = 712, Y-bar = 83.4, S = 18.7. For males 75+ years old, n = 1001, Y-bar = 78.5, S = 19.0

Do the data provide evidence that the younger male population weighs more (on average) than the older male population? (Note that here the data are given in a summarized form, unlike the previous problem, where the raw data were given.)

Here is a figure that summarizes this example:

Note that we defined the younger age group and the older age group as population 1 and population 2, respectively, and μ₁ and μ₂ as the mean weight of population 1 and population 2, respectively.

Step 1:

Since we want to test whether the older age group (population 2) weighs less on average than the younger age group (population 1), we are testing:

H_0: μ_1 - μ_2 = 0, H_a: μ_1 - μ_2 > 0

or equivalently,

H_0: μ_1 = μ_2, H_a: μ_1 > μ_2

Step 2:

We can safely use the two-sample t-test in this case since:

The samples are independent, since each of the samples was chosen at random.
Both sample sizes are very large (712 and 1,001), and therefore we can proceed regardless of whether the populations are normal or not.

It is possible from these data to calculate the t-statistic of 5.31 and the p-value of 0.000. The t-value is quite large, and the p-value correspondingly small, indicating that our data are very different from what is claimed in the null hypothesis.

Step 3:

The p-value is essentially 0, indicating that it would be nearly impossible to observe a difference between the sample mean weights of 4.9 (or more) if the mean weights in the age group populations were the same (i.e., if H_o were true).

Step 4:

A p-value of 0 (or very close to it) indicates that the data provide strong evidence against H_o, so we reject it and conclude that the mean weight of males 20-29 years old is higher than the mean weight of males 75 years old and older. In other words, males in the younger age group weigh more, on average, than males in the older age group.

Confidence Interval for (Two-Sample t Confidence Interval)

So far we’ve discussed the two-sample t-test, which checks whether there is enough evidence stored in the data to reject the claim that $μ_{1} - μ_{2} = 0$ (or equivalently, that $μ_{1} = μ_{2}$ ) in favor of one of the three possible alternatives.

If we would like to estimate $μ_{1} - μ_{2}$ we can use the natural point estimate, $¯ ¯ ¯ y_{1} - ¯ ¯ ¯ y_{2}$ , or preferably, a 95% confidence interval which will provide us with a set of plausible values for the difference between the population means $μ_{1} - μ_{2}$ .

In particular, if the test has rejected $H_{o} : μ_{1} - μ_{2} = 0$ , a confidence interval for $μ_{1} - μ_{2}$ can be insightful since it quantifies the effect that the categorical explanatory variable has on the response.

Comment

We will not go into the formula and calculation of the confidence interval, but rather ask our software to do it for us, and focus on interpretation.

Example

Recall our leading example about the looks vs. personality score of females and males:

The Gender(X) Variable has two categories, which gives us Population 1: Females and Population 2: Males. Each population has its own Y-Mean μ, so population 1's mean is μ_1 and population 2's mean is μ_2. For each population we take an SRS. For Population 1, an SRS of size 150 is taken, and for population 2 an SRS of size 85 is taken.

Here again is the output:

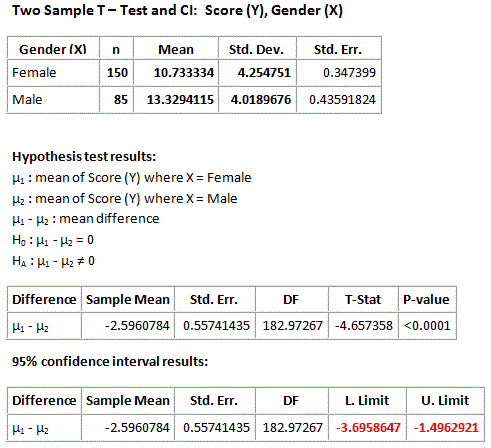
Recall that we rejected the null hypothesis in favor of the two-sided alternative and concluded that the mean score of females is different from the mean score of males. It would be interesting to supplement this conclusion with more details about this difference between the means, and the 95% confidence interval for $μ_{1} - μ_{2}$ does exactly that.

According to the output the 95% confidence interval for $μ_{1} - μ_{2}$ is roughly (-3.7, -1.5). First, note that the confidence interval is strictly negative suggesting that μ₁ is lower than μ₂ . Furthermore, the confidence interval tells me that we are 95% confident that the mean “looks vs. personality score” of females ( μ₁ ) is between 1.5 and 3.7 points lower than the mean looks vs. personality score of males ( μ₂ ). The confidence interval therefore quantifies the effect that the explanatory variable (gender) has on the response (looks vs personality score).

Comment

As we’ve seen in previous tests, as well as in the two-samples case, the 95% confidence interval for $μ_{1} - μ_{2}$ can be used for testing in the two-sided case ( $H_{o} : μ_{1} - μ_{2} = 0$ vs. $H_{a} : μ_{1} - μ_{2} \neq 0$ ):

If the null value, 0, falls outside the confidence interval, H_o is rejected

If the null value, 0, falls inside the confidence interval, H_o is not rejected

Example

Let’s go back to our leading example of the looks vs. personality score where we had a two-sided test.

Two Sample T - Test and CI: Score(Y),Gender (X) Summary statistics for Score (Y): For Gender(X) = Female: n = 150, Mean = 10.733334, Std. Dev. = 4.254751, Std. Err. = 0.347399 For Gender(X) = Male: n = 85, Mean = 13.3294115, Std. Dev. = 4.0189676, Std. Err. = 0.43591824 Hypothesis test results: μ_1: mean of score (Y) where X = Female. μ_2: mean of score (Y) where X = Male. μ_1 - μ_2: mean difference. H_0: μ_1 - μ_2 = 0, H_A: μ_1 - μ_2 ≠ 0 Difference: μ_1 - μ_2 Sample Mean: -2.5960784 Std. Err.: 0.55741435 DF: 182.97267 T-Stat: -4.657358 P-Value: < 0.0001 95% Confidence Interval Results: Difference: μ_1 - μ_2 Sample Mean: -2.5960784 Std. Err.: 0.55741435 DF: 182.97267 L. Limit: -3.6958647 U. Limit: -1.4962921

We used the fact that the p-value is so small to conclude that Ho can be rejected. We can also use the confidence interval to reach the same conclusion since 0 falls outside the confidence interval. In other words, since 0 is not a plausible value for $μ_{1} - μ_{2}$ we can reject H_o, which claims that $μ_{1} - μ_{2} = 0$ .

Did I get this?

Below you’ll find three sample outputs of the two-sided two-sample t-test:

H_0: μ_1 - μ_2 = 0 vs. H_a: μ_1 - μ_2 ≠ 0

However, only one of the outputs could be correct (the other two contain an inconsistency). Your task is to decide which of the following outputs is the correct one (Hint: No calculations are necessary in order to answer this question. Instead pay attention to the p-value and confidence interval).

Output A:
- p-value: 0.289
- 95% Confidence Interval: (-5.93090, -1.78572)

Output B:
- p-value: 0.003
- 95% Confidence Interval: (-13.97384, 2.89733)

Output C:
- p-value: 0.223
- 95% Confidence Interval: (-9.31432, 2.20505)

Let’s Summarize

We have completed our discussion of the two-sample t-test for comparing two populations’ means when the samples are independent. Let’s summarize what we have learned.

The two sample t-test is used for comparing the means of a quantitative variables (Y) in two populations (which we initially called sub-populations).
Our goal is comparing μ₁ and μ₂ (which in practice is done by making inference on the difference μ₁ – μ₂). The null hypotheses is
- Ho: μ₁ – μ₂ = 0
and the alternative hypothesis is one of the following (depending on the context of the problem):
- Ha: μ₁ – μ₂ < 0
- Ha: μ₁ – μ₂ > 0
- Ha: μ₁ – μ₂ ≠ 0
The two-sample t-test can be safely used when the samples are independent and at least one of the following two conditions hold:
- The variable Y is known to have a normal distribution in both populations
- The two sample sizes are large.
When the sample sizes are not large (and we therefore need to check the normality of Y in both population), what we do in practice is look at the histograms of the two samples and make sure that there are no signs of non-normality such as extreme skewedness and/or outliers.
The test statistic is as follows and has a t distribution when the null hypothesis is true:
P-values are obtained from the output, and conclusions are drawn as usual, comparing the p-value to the significance level alpha.
If H_o is rejected, a 95% confidence interval for μ₁ – μ₂ can be very insightful and can also be used for the two-sided test.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intro to Statistics MAT1260 by SBCCOE is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Comparing Two Means—Two Independent Samples (The Two-Sample t-Test)

Overview

The Two-Sample t-Test

Step 1: Stating the Hypotheses

Comment

Step 2: Check Conditions, and Summarize the Data Using a Test Statistic

Comment

Step 3: Finding the p-value of the test

Step 4: Conclusion in context

Comments

Confidence Interval for (Two-Sample t Confidence Interval)

Comment

Comment

Let’s Summarize

License

Share This Book