11.2: Chi-Squared Test for Independence
Overview
The last three procedures that we studied (two-sample t, paired t, and ANOVA) all involve the relationship between a categorical explanatory variable and a quantitative response variable, corresponding to Case C→Q in the role/type classification table below. Next, we will consider inferences about the relationships between two categorical variables, corresponding to case C→C.

In the Exploratory Data Analysis unit of the course, we summarized the relationship between two categorical variables for a given data set (using a two-way table and conditional percents), without trying to generalize beyond the sample data.
Now we perform statistical inference for two categorical variables, using the sample data to draw conclusions about whether or not we have evidence that the variables are related in the larger population from which the sample was drawn. In other words, we would like to assess whether the relationship between X and Y that we observed in the data is due to a real relationship between X and Y in the population or if it is something that could have happened just by chance due to sampling variability.

The statistical test that will answer this question is called the chi-square test for independence. Chi is a Greek letter that looks like this: [latex]\chi[/latex], so the test is sometimes referred to as: The [latex]\chi ^{2}[/latex] test for independence.
The structure of this section will be very similar to that of the previous ones in this module. We will first present our leading example, and then introduce the chi-square test by going through its 4 steps, illustrating each one using the example. We will conclude by presenting another complete example. As usual, you’ll have activities along the way to check your understanding, and to learn how to use software to carry out the test.
Let’s start with our leading example.
Example
In the early 1970s, a young man challenged an Oklahoma state law that prohibited the sale of 3.2% beer to males under age 21 but allowed its sale to females in the same age group. The case (Craig v. Boren, 429 U.S. 190, 1976) was ultimately heard by the U.S. Supreme Court.
The main justification provided by Oklahoma for the law was traffic safety. One of the 3 main pieces of data presented to the court was the result of a “random roadside survey” that recorded information on gender, and whether or not the driver had been drinking alcohol in the previous two hours. There were a total of 619 drivers under 20 years of age included in the survey.
Here is what the collected data looked like:

The following two-way table summarizes the observed counts in the roadside survey:

Our task is to assess whether these results provide evidence of a significant (“real”) relationship between gender and drunk driving.
The following figure summarizes this example:

Note that as the figure stresses, since we are looking to see whether drunk driving is related to gender, our explanatory variable (X) is gender, and the response variable (Y) is drunk driving. Both variables are two-valued categorical variables, and therefore our two-way table of observed counts is 2-by-2. It should be mentioned that the chi-square procedure that we are going to introduce here is not limited to 2-by-2 situations, but can be applied to any r-by-c situation where r is the number of rows (corresponding to the number of values of one of the variables) and c is the number of columns (corresponding to the number of values of the other variable).
Before we introduce the chi-square test, let’s conduct an exploratory data analysis (that is, look at the data to get an initial feel for it). By doing that, we will also get a better conceptual understanding of the role of the test.
Exploratory Analysis
Recall that the key to reporting appropriate summaries for a two-way table is deciding which of the two categorical variables plays the role of explanatory variable, and then calculating the conditional percentages — the percentages of the response variable for each value of the explanatory variable — separately. In this case, since the explanatory variable is gender, we would calculate the percentages of drivers who did (and did not) drink alcohol for males and females separately.
Here is the table of conditional percentages:

For the 619 sampled drivers, a larger percentage of males were found to be drunk than females (16.0% vs. 11.6%). Our data, in other words, provide some evidence that drunk driving is related to gender; however, this in itself is not enough to conclude that such a relationship exists in the larger population of drivers under 20. We need to further investigate the data and decide between the following two points of view:
-
The evidence provided by the roadside survey (16% vs 11.6%) is strong enough to conclude (beyond a reasonable doubt) that it must be due to a relationship between drunk driving and gender in the population of drivers under 20.
-
The evidence provided by the roadside survey (16% vs. 11.6%) is not strong enough to make that conclusion, and could have happened just by chance, due to sampling variability, and not necessarily because a relationship exists in the population.
Actually, these two opposing points of view constitute the null and alternative hypotheses of the chi-square test for independence, so now that we understand our example and what we still need to find out, let’s introduce the four-step process of this test.
Learn by Doing
The purpose of this activity is to introduce you to the example that you are going to work through in this section, and for you to get a feeling for the data by conducting exploratory analysis.
Background: Alcoholism Risk in 9/11 Responders
Among firefighters and other “first responders” to the World Trade Center on September 11, 2001, there have been reports of increased alcohol-related difficulties (e.g., DUI). A survey of 9/11 first responders (On the Front Line: The Work of First Responders in a Post-9/11 World) conducted by Cornell researcher Samuel Bacharach was released in 2004. To see the report: Firefighter Stress. Based on the research, we can construct the following two-way table of observed counts:

Using the data from this research, we would like to investigate whether alcohol risk among New York firefighters is significantly related to participation in the 9/11 rescue.
There are two categorical variables in this problem:
* Alcohol risk (none, moderate to severe)
* Participation in the 9/11 rescue (yes, no)
The Chi-Square Test for Independence
The chi-square test for independence examines our observed data and tells us whether we have enough evidence to conclude beyond a reasonable doubt that two categorical variables are related. Much like the previous part on the ANOVA F-test, we are going to introduce the hypotheses (step 1), and then discuss the idea behind the test, which will naturally lead to the test statistic (step 2). Let’s start.
Step 1: Stating the hypotheses
Unlike all the previous tests that we presented, the null and alternative hypotheses in the chi-square test are stated in words rather than in terms of population parameters. They are:
Ho: There is no relationship between the two categorical variables. (They are independent.)
Ha: There is a relationship between the two categorical variables. (They are not independent.)
Example
In our example, the null and alternative hypotheses would then state:
Ho: There is no relationship between gender and drunk driving.
Ha: There is a relationship between gender and drunk driving.
Or equivalently,
Ho: Drunk driving and gender are independent
Ha: Drunk driving and gender are not independent
and hence the name “chi-square test for independence.”
Comment
Algebraically, independence between gender and driving drunk is equivalent to having equal proportions who drank (or did not drink) for males vs. females. In fact, the null and alternative hypotheses could have been re-formulated as
Ho: proportion of male drunk drivers = proportion of female drunk drivers
Ha: proportion of male drunk drivers ≠ proportion of female drunk drivers
However, expressing the hypotheses in terms of proportions works well and is quite intuitive for two-by-two tables, but the formulation becomes very cumbersome when at least one of the variables has several possible values, not just two. We are therefore going to always stick with the “wordy” form of the hypotheses presented in step 1 above.
The Idea of the Chi-Square Test
The idea behind the chi-square test, much like previous tests that we’ve introduced, is to measure how far the data are from what is claimed in the null hypothesis. The further the data are from the null hypothesis, the more evidence the data presents against it. We’ll use our data to develop this idea. Our data are represented by the observed counts:

How will we represent the null hypothesis?
In the previous tests we introduced, the null hypothesis was represented by the null value. Here there is not really a null value, but rather a claim that the two categorical variables (drunk driving and gender, in this case) are independent.
To represent the null hypothesis, we will calculate another set of counts — the counts that we would expect to see (instead of the observed ones) if drunk driving and gender were really independent (i.e., if Ho were true). For example, we actually observed 77 males who drove drunk; if drunk driving and gender were indeed independent (if Ho were true), how many male drunk drivers would we expect to see instead of 77? Similarly, we can ask the same kind of question about (and calculate) the other three cells in our table.
In other words, we will have two sets of counts:
-
the observed counts (the data)
-
the expected counts (if Ho were true)
We will measure how far the observed counts are from the expected ones. Ultimately, we will base our decision on the size of the discrepancy between what we observed and what we would expect to observe if Ho were true.
How are the expected counts calculated? Once again, we are in need of probability results. Recall from the probability section that if events A and B are independent, then P(A and B) = P(A) * P(B). We use this rule for calculating expected counts, one cell at a time.
Here again are the observed counts:

Applying the rule to the first (top left) cell, if driving drunk and gender were independent then:
P(drunk and male) = P(drunk) * P(male)
By dividing the counts in our table, we see that:
P(Drunk) = 93 / 619 and
P(Male) = 481 / 619,
and so,
P(Drunk and Male) = (93 / 619) (481 / 619)
Therefore, since there are total of 619 drivers, if drunk driving and gender were independent, the count of drunk male drivers that I would expect to see is:
[latex]619*P(Drunk\ and\ Male)=619\left ( \frac{93}{619} \right )\left ( \frac{481}{619} \right )=\frac{93*481}{619}[/latex]
Notice that this expression is the product of the column and row totals for that particular cell, divided by the overall table total.
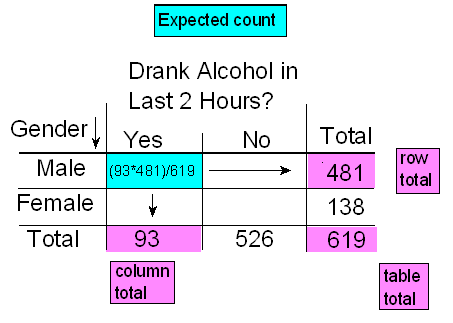
Similarly, if the variables are independent,
P(Drunk and Female) = P(Drunk) * P(Female) = (93 / 619) (138 / 619)
and the expected count of females driving drunk would be
[latex]\left(\frac{93}{619}\right)\left(\frac{138}{619}\right)=\frac{93\ast138}{619}[/latex]
Again, the expected count equals the product of the corresponding column and row totals, divided by the overall table total:

This will always be the case, and will help streamline our calculations:
[latex]Expected\ Count=\frac{Column\ total\ \ast Row\ total}{Table\ total}[/latex]
Learn by Doing
Here is the complete table of expected counts, followed by the table of observed counts:


Did I get this?
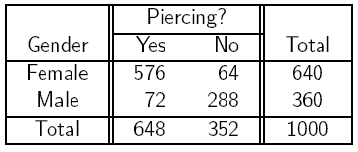
A study was done on the relationship between gender and piercing among high-school students. A sample of 1,000 students was chosen, then classified according to gender and according to whether or not they had any of their ears pierced. The results of the study are summarized in the following 2-by-2 table:
We see that there are differences between the observed and expected counts in the respective cells. We now have to come up with a measure that will quantify these differences. This is the chi-square test statistic.
Step 2: Checking the Conditions and Calculating the Test Statistic
Given our discussion on the previous page, it would be natural to present the test statistic, and then come back to the conditions that allow us to safely use the chi-square test, although in practice this is done the other way around.
The single number that summarizes the overall difference between observed and expected counts is the chi-square statistic χ2 , which tells us in a standardized way how far what we observed (data) is from what would be expected if Ho were true.
Here it is:
[latex]\mathcal{X}^2=\sum_{all\ cells}\frac{\left(Observed\ Count-Expected\ Count\right)^2}{Expected\ Count}[/latex]
Comment
As we expected, χ2 is based on each of the differences: observed count – expected count (one such difference for each cell), but why is it squared? Why do we divide each square difference by the expected count? The reason we do that is so that the null distribution of χ2 will have a known null distribution (under which p-values can be easily calculated). The details are really beyond the scope of this course, but we will just say that the null distribution of χ2 is called chi-square (which is not very surprising given that the test is called the chi-square test), and like the t-distributions there are many chi-square distributions distinguished by the number of degrees of freedom associated with them.
Conditions under Which the Chi-Square Test Can Safely Be Used
-
The sample should be random.
-
In general, the larger the sample, the more accurate and reliable the test results are. There are different versions of what the conditions are that will ensure reliable use of the test, all of which involve the expected counts. One version of the conditions says that all expected counts need to be greater than 1, and at least 80% of expected counts need to be greater than 5. A more conservative version requires that all expected counts are larger than 5.
Example
Here, again, are the observed and expected counts.

Checking the conditions:
-
The roadside survey is known to have been random.
-
All the expected counts are above 5.
We can therefore safely proceed with the chi-square test, and the chi-square test statistic is:
[latex]\frac{\left(77-72.3\right)^2}{72.3}+\frac{\left(404-408.7\right)^2}{408.7}+\frac{\left(16-20.7\right)^2}{20.7}+\frac{\left(122-117.3\right)^2}{117.3}=.306+.054+1.067+.188=1.62[/latex]
Did I get this?
A study was done on the relationship between gender and piercing among high-school students. A sample of 1,000 students was chosen, and then classified according to both gender and whether or not they had either of their ears pierced. The following (edited) StatCrunch output is available:
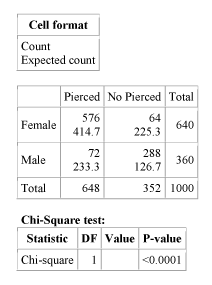
Comment
Once the chi-square statistic has been calculated, we can get a feel for its size: is there a relatively large difference between what we observed and what the null hypothesis claims, or a relatively small one? It turns out that for a 2-by-2 case like ours, we are inclined to call the chi-square statistic “large” if it is larger than 3.84. Therefore, our test statistic is not large, indicating that the data are not different enough from the null hypothesis for us to reject it (we will also see that in the p-value not being small). For other cases (other than 2-by-2) there are different cut-offs for what is considered large, which are determined by the null distribution in that case. We are therefore going to rely only on the p-value to draw our conclusions. Even though we cannot really use the chi-square statistic, it was important to learn about it, since it encompasses the idea behind the test.
Did I get this?
The purpose of this activity is to continue to explore whether the risk of alcohol problems among New York firefighters and first responders is related to participation in the 911 rescue. In particular, in this activity, we will state the hypotheses that are being tested, learn how to carry out the chi-square test for independence using statistical software, and check whether the conditions under which this test can be safely used are met.
| Observed data | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
New York Firefighters and first responders
|
||||||||||||||||
|
Step 3: Finding the p-value
The p-value for the chi-square test for independence is the probability of getting counts like those observed, assuming that the two variables are not related (which is what is claimed by the null hypothesis). The smaller the p-value, the more surprising it would be to get counts like we did, if the null hypothesis were true.
Technically, the p-value is the probability of observing χ2 at least as large as the one observed. Using statistical software, we find that the p-value for this test is 0.201.
Step 4: Stating the conclusion in context
As usual, we use the magnitude of the p-value to draw our conclusions. A small p-value indicates that the evidence provided by the data is strong enough to reject Ho and conclude (beyond a reasonable doubt) that the two variables are related. In particular, if a significance level of .05 is used, we will reject Ho if the p-value is less than .05.
Example
A p-value of .201 is not small at all. There is no compelling statistical evidence to reject Ho, and so we will continue to assume it may be true. Gender and drunk driving may be independent, and so the data suggest that a law that forbids sale of 3.2% beer to males and permits it to females is unwarranted. In fact, the Supreme Court, by a 7-2 majority, struck down the Oklahoma law as discriminatory and unjustified. In the majority opinion Justice Brennan wrote (http://www.law.umkc.edu/faculty/projects/ftrials/conlaw/craig.html):
“Clearly, the protection of public health and safety represents an important function of state and local governments. However, appellees’ statistics in our view cannot support the conclusion that the gender-based distinction closely serves to achieve that objective and therefore the distinction cannot under [prior case law] withstand equal protection challenge.”
The purpose of this activity is to draw our conclusion regarding the relationship between participation in the 9/11 rescue and risk of alcohol problems among New York firefighters and first responders.
In the previous activity, we created a table of expected counts to go along with our table of observed counts. In this activity, we will use both tables to conduct a chi-square test on the data.
To do this in Excel, we first need to re-create both the table of observed counts and table of expected counts from the last exercise. Here are the data again for your convenience:
In the previous activity, we carried out the chi-square test using StatCrunch and obtained the following output:
Contingency table results:
Rows: 911
Columns: None
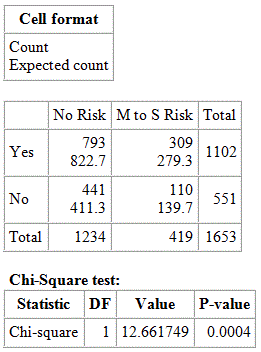
Learn by Doing
Comment
This is a good opportunity to illustrate an important idea that was discussed earlier in this unit: The larger the sample the results are based on, the more evidence they carry. Let’s take the previous example and simply multiply each of the counts by 3:

and see what would have happened if these were the original data. Obviously, the conditional counts would remain the same:

In other words, the sample provides the “same” results, but this time they are based on a much larger sample (1857 instead of 619). This is reflected by the chi-square test. In this case, software gives us a chi-square statistic of 4.910 and a p-value of 0.027.
As before, Ho states that gender and drunk driving are not related; Ha states that they are related. Since the observed counts are triple what they were before, the expected counts are also tripled. When done with software the original chi-square statistic was 1.637 since software doesn’t round as much. The chi-square statistic when we tripled the data is 3 times 1.637, or 4.91 (which now is in the “large” range). Therefore, the p-value is smaller and is now .027.
Now, we do reject Ho, and we conclude that gender and drunk driving are related. In this case, the “largest contribution to chi-square” is large enough to provide evidence of a relationship. This is due to the fact that so few females drove drunk (48) compared to the number that would be expected (62.2, which is 414 * 279 / 1857) if the variables gender and drunk driving were not related. This contribution is [latex]\frac{\left(48-62.2\right)^2}{62.2}=3.242[/latex].
Let’s look at another example.
Example
Steroid Use in Sports
Major-league baseball star Barry Bonds admitted to using a steroid cream during the 2003 season. Is steroid use different in baseball than in other sports? According to the 2001 National Collegiate Athletic Association (NCAA) survey (http://www.ncaa.org/library/research/substance_use_habits/2001/substance_use_habits.pdf), which is self-reported and asked of a stratified random selection of teams from each of the three NCAA divisions, reported steroid use among the top 5 college sports was as follows:

Do the data provide evidence of a significant relationship between steroid use and the type of sport? In other words, are there significant differences in steroid use among the different sports?
Before we carry out the chi-square test for independence, let’s get a sense of the data by calculating the conditional percents:

It seems as if there are differences in steroid use among the different sports. Even though the differences do not seem to be overwhelming, since the sample size is so large, these differences might be significant. Let’s carry out the test and see.
Step 1: Stating the hypotheses
The hypotheses are:
Ho: steroid use is not related to the type of sport (or: type of sport and steroid use are independent)
Ha: Steroid use is related to the type of sport (or: type of sport and steroid use are not independent).
Step 2: Checking conditions and finding the test statistic
Here is the Minitab output of the chi-square test for this example:

-
Conditions:
-
We are told that the sample was random.
-
All the expected counts are above 5.
-
-
Test statistic:
The test statistic is 14.626. Note that the “largest contributors” to the test statistic are 5.729 and 3.990. The first cell corresponds to football players who used steroids, with an observed count larger than we would expect to see under independence. The second cell corresponds to tennis players who used steroids, and has an observed count lower than we would expect under independence.
Step 3: Finding the p-value
According to the output p-value it would be extremely unlikely (probability of 0.006) to get counts like those observed if the null hypothesis were true. In other words, it would be very surprising to get data like those observed if steroid use were not related to sport type.
Step 4: Conclusion
The small p-value indicates that the data provide strong evidence against the null hypothesis, so we reject it and conclude that the steroid use is related to the type of sport.
Let’s Summarize
-
The chi-square test for independence is used to test whether the relationship between two categorical variables is significant. In other words, the chi-square procedure assesses whether the data provide enough evidence that a true relationship between the two variables exists in the population.
-
The hypotheses that are being tested in the chi-square test for independence are:
-
Ho: There is no relationship between … and ….
-
Ha: There is a relationship between … and ….
-
or equivalently,
-
Ho: The variables … and … are independent.
-
Ha: The variables … and … are not independent.
-
-
The idea behind the test is measuring how far the observed data are from the null hypothesis by comparing the observed counts to the expected counts—the counts that we would expect to see (instead of the observed ones) had the null hypothesis been true. The expected count of each cell is calculated as follows:

-
The measure of the difference between the observed and expected counts is the chi-square test statistic, whose null distribution is called the chi-square distribution. The chi-square test statistic is calculated as follows:

-
Once we verify that the conditions that allow us to safely use the chi-square test are met, we use software to carry it out and use the p-value to guide our conclusions.

