11.1: ANOVA
Learning Objectives
- In a given context, carry out the inferential method for comparing groups and draw the appropriate conclusions.
- Specify the null and alternative hypotheses for comparing groups.
Comparing More Than Two Means—ANOVA
Overview
In this part, we continue to handle situations involving one categorical explanatory variable and one quantitative response variable, which is case C→Q in our role/type classification table:

So far we have discussed the two samples and matched pairs designs, in which the categorical explanatory variable is two-valued. As we saw, in these cases, examining the relationship between the explanatory and the response variables amounts to comparing the mean of the response variable (Y) in two populations, which are defined by the two values of the explanatory variable (X). The difference between the two samples and matched pairs designs is that in the former, the two samples are independent, and in the latter, the samples are dependent.
We are now moving on to cases in which the categorical explanatory variable takes more than two values. Here, as in the two-valued case, making inferences about the relationship between the explanatory (X) and the response (Y) variables amounts to comparing the means of the response variable in the populations defined by the values of the explanatory variable, where the number of means we are comparing depends, of course, on the number of values of X. Unlike the two-valued case, where we looked at two sub-cases (1) when the samples are independent (two samples design) and (2) when the samples are dependent (matched pairs design, here, we are just going to discuss the case where the samples are independent. In other words, we are just going to extend the two samples design to more than two independent samples.

Comment
The extension of the matched pairs design to more than two dependent samples is called “Repeated Measures” and is beyond the scope of this course.
The inferential method for comparing more than two means that we will introduce in this part is called Analysis Of Variance (abbreviated as ANOVA), and the test associated with this method is called the ANOVA F-test. The structure of this part will be very similar to that of the previous two. We will first present our leading example, and then introduce the ANOVA F-test by going through its 4 steps, illustrating each one using the example. (It will become clear as we explain the idea behind the test where the name “Analysis of Variance” comes from.) We will then present another complete example, and conclude with some comments about possible follow-ups to the test. As usual, you’ll have activities along the way to check your understanding, and learn how to use software to carry out the test.
Let’s start by introducing our leading example.
Example
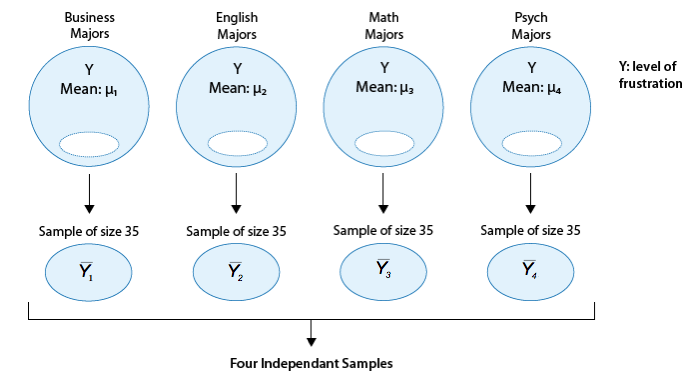
Is “academic frustration” related to major?
A college dean believes that students with different majors may experience different levels of academic frustration. Random samples of size 35 of Business, English, Mathematics, and Psychology majors are asked to rate their level of academic frustration on a scale of 1 (lowest) to 20 (highest).

The figure highlights what we have already mentioned: examining the relationship between major (X) and frustration level (Y) amounts to comparing the mean frustration levels ([latex]\mu _{1}, \mu _{2},\mu _{3},\mu _{4}[/latex]) among the four majors defined by X. Also, the figure reminds us that we are dealing with a case where the samples are independent.
Comment
There are two ways to record data in the ANOVA setting:
-
Unstacked: One column for each of the four majors, with each column listing the frustration levels reported by all sampled students in that major:
Business
English
Math
Psychology
11
11
9
11
6
9
16
19
6
14
11
13
etc.
-
Stacked: one column for all the frustration levels, and next to it a column to keep track of which major a student is in:
Frustration(Y)
Major(X)
9
Business
2
Business
9
Business
10
English
11
Psychology
13
English
13
Psychology
12
Math
etc.
The “unstacked” format helps us to look at the four groups separately, while the “stacked” format helps us remember that there are, in fact, two variables involved: frustration level (the quantitative response variable) and major (the categorical explanatory variable).
To open Excel with the data in the worksheet, right click to download the frustration file to your computer. Then find the downloaded file and double-click it to open it in Excel. When Excel opens you may have to enable editing.
Note that in the first 4 columns (A-D), the data are in unstacked format, and in the next two columns (E-F) the data are stacked.
The ANOVA F-test
Now that we understand in what kind of situations ANOVA is used, we are ready to learn how it works, or more specifically, what the idea is behind comparing more than two means. As we mentioned earlier, the test that we will present is called the ANOVA F-test, and as you’ll see, this test is different in two ways from all the tests we have presented so far:
- Unlike the previous tests, where we had three possible alternative hypotheses to choose from (depending on the context of the problem), in the ANOVA F-test there is only one alternative, which actually makes life simpler.
- The test statistic will not have the same structure as the test statistics we’ve seen so far. In other words, it will not have the form: [latex]\frac{sample\ statistic-null\ value}{standard\ error}[/latex], but a different structure that captures the essence of the F-test, and clarifies where the name “analysis of variance” is coming from.
Let’s start.
Step 1: Stating the Hypotheses
The null hypothesis claims that there is no relationship between X and Y. Since the relationship is examined by comparing [latex]\mu _{1},\mu _{2},\mu _{3},...,\mu _{k}[/latex], the means of Y in the populations defined by the values of X, no relationship would mean that all the means are equal. Therefore the null hypothesis of the F-test is: [latex]H_{0}=\mu _{1}=\mu _{2}=\mu _{3}=...=\mu _{k}[/latex]
As we mentioned earlier, here we have just one alternative hypothesis, which claims that there is a relationship between X and Y. In terms of the means [latex]\mu _{1},\mu _{2},\mu _{3},...,\mu _{k}[/latex], it simply says the opposite of the alternative, that not all the means are equal, and we simply write: Ha: not all the μ’s are equal.
Example
Recall our “Is academic frustration related to major?” example:

Learn by Doing
The hypotheses that are being tested in our example are:
Ho: μ1 = μ2 = μ3 = μ4
Ha: μ1 ≠ μ2 ≠ μ3 ≠ μ4
The correct hypotheses for our example are:

Note that there are many ways for [latex]\mu _{1},\mu _{2},\mu _{3},\mu _{4}[/latex] not to be all equal, and [latex]\mu _{1}\neq \mu _{2}\neq \mu _{3}\neq \mu _{4}[/latex] is just one of them. Another way could be [latex]\mu _{1}= \mu _{2}= \mu _{3}\neq \mu _{4}[/latex] or [latex]\mu _{1}= \mu _{2}\neq \mu _{3}= \mu _{4}[/latex]. The alternative of the ANOVA F-test simply states that not all of the means are equal, and is not specific about the way in which they are different.
The idea behind the ANOVA F-Test
Let’s think about how we would go about testing whether the population means [latex]\mu _{1},\mu _{2},\mu _{3},\mu _{4}[/latex] are equal. It seems as if the best we could do is to calculate their point estimates—the sample mean in each of our 4 samples (denote them by [latex]\overline{y_{1}},\overline{y_{2}},\overline{y_{3}},\overline{y_{4}}[/latex]),
and see how far apart these sample means are, or in other words, measure the variation between the sample means. If we find that the four sample means are not all close together, we’ll say that we have evidence against Ho, and otherwise, if they are close together, we’ll say that we do not have evidence against Ho. This seems quite simple, but is this enough? Let’s see.
It turns out that:
* The sample mean frustration score of the 35 business majors is: [latex]\overline{y_{1}}=7.3[/latex]
* The sample mean frustration score of the 35 English majors is: [latex]\overline{y_{2}}=11.8[/latex]
* The sample mean frustration score of the 35 math majors is: [latex]\overline{y_{3}}=13.2[/latex]
* The sample mean frustration score of the 35 psychology majors is: [latex]\overline{y_{4}}=14.0[/latex]
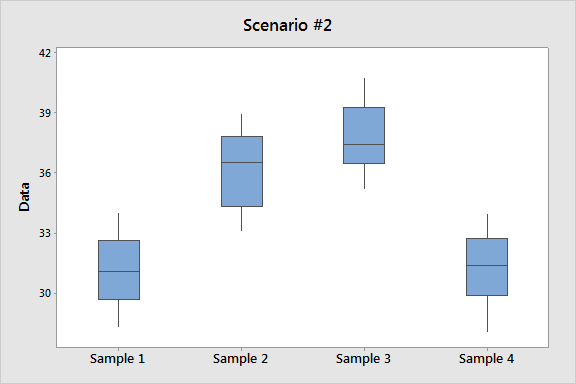
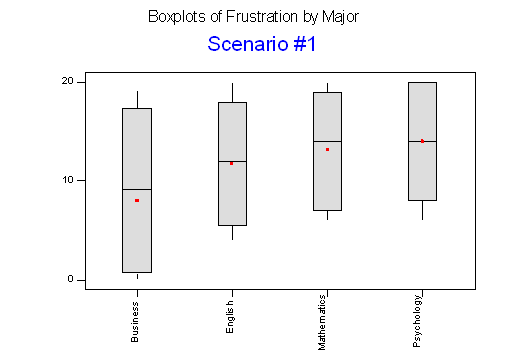
Below we present two possible scenarios for our example. In both cases, we construct side-by-side boxplots for four groups of frustration levels that have the same variation among their means. Thus, Scenario #1 and Scenario #2 both show data for four groups with the sample means 7.3, 11.8, 13.2, and 14.0 (indicated with red marks).

Learn by Doing
The important difference between the two scenarios is that the first represents data with a large amount of variation within each of the four groups; the second represents data with a small amount of variation within each of the four groups.
Scenario 1, because of the large amount of spread within the groups, shows boxplots with plenty of overlap. One could imagine the data arising from 4 random samples taken from 4 populations, all having the same mean of about 11 or 12. The first group of values may have been a bit on the low side, and the other three a bit on the high side, but such differences could conceivably have come about by chance. This would be the case if the null hypothesis, claiming equal population means, were true. Scenario 2, because of the small amount of spread within the groups, shows boxplots with very little overlap. It would be very hard to believe that we are sampling from four groups that have equal population means. This would be the case if the null hypothesis, claiming equal population means, were false.
Thus, in the language of hypothesis tests, we would say that if the data were configured as they are in scenario 1, we would not reject the null hypothesis that population mean frustration levels were equal for the four majors. If the data were configured as they are in scenario 2, we would reject the null hypothesis, and we would conclude that mean frustration levels differ, depending on major.
Let’s summarize what we learned from this. The question we need to answer is: Are the differences among the sample means ([latex]\overline{Y}[/latex]‘s) due to true differences among the μ’s (alternative hypothesis), or merely due to sampling variability (null hypothesis)?
In order to answer this question using our data, we obviously need to look at the variation among the sample means, but this alone is not enough. We need to look at the variation among the sample means relative to the variation within the groups. In other words, we need to look at the quantity:

which measures to what extent the difference among the sampled groups’ means dominates over the usual variation within sampled groups (which reflects differences in individuals that are typical in random samples).
When the variation within groups is large (like in scenario 1), the variation (differences) among the sample means could become negligible and the data provide very little evidence against Ho. When the variation within groups is small (like in scenario 2), the variation among the sample means dominates over it, and the data have stronger evidence against Ho.
Looking at this ratio of variations is the idea behind the comparing more than two means; hence the name analysis of variance (ANOVA).
Now that we understand the idea behind the ANOVA F-test, let’s move on to step 2. We’ll start by talking about the test statistic, since it will be a natural continuation of what we’ve just discussed, and then move on to talk about the conditions under which the ANOVA F-test can be used. In practice, however, the conditions need to be checked first, as we did before.
Step 2: Checking Conditions and Finding the Test Statistic
The test statistic of the ANOVA F-test, called the F statistic, has the form

It has a different structure from all the test statistics we’ve looked at so far, but it is similar in that it is still a measure of the evidence against H0. The larger F is (which happens when the denominator, the variation within groups, is small relative to the numerator, the variation among the sample means), the more evidence we have against H0.
Did I get this?
Consider the following generic situation:

In this case, we are testing
-
H0: μ1 = μ2 = μ3
-
Ha: Not all the μ’s are equal
The following are two possible scenarios of the data (note in both scenarios the sample means are 25, 30, and 35).


Learn by Doing
Suppose that we would like to compare four populations (for example, four races/ethnicities or four age groups) with respect to a certain psychological test score. More specifically we would like to test
-
H0: μ1 = μ2 = μ3 = μ3
-
Ha: Not all the μ’s are equal
where μ1 is the mean test score in population 1, μ2 is the mean test score in population 2, μ3 is the mean test score in population 3, and μ4 is the mean test score in population 4.
We take a random sample from each population and use these four independent samples in order to carry out the test.
The following are two possible scenarios for the data:
|
Note that in both scenarios, the score averages of the four samples are very similar.
Comments
-
The focus here is for you to understand the idea behind this test statistic, so we do not go into detail about how the two variations are measured. We instead rely on software output to obtain the F-statistic.
-
This test is called the ANOVA F-test. So far, we have explained the ANOVA part of the name. Based on the previous tests we introduced, it should not be surprising that the “F-test” part comes from the fact that the null distribution of the test statistic, under which the p-values are calculated, is called an F-distribution. We will say very little about the F-distribution in this course, which will essentially be limited to this comment and the next one.
-
It is fairly straightforward to decide if a z-statistic is large. Even without tables, we should realize by now that a z-statistic of 0.8 is not especially large, whereas a z-statistic of 2.5 is large. In the case of the t-statistic, it is less straightforward, because there is a different t-distribution for every sample size n (and degrees of freedom n − 1). However, the fact that a t-distribution with a large number of degrees of freedom is very close to the z (standard normal) distribution can help to assess the magnitude of the t-test statistic.
When the size of the F-statistic must be assessed, the task is even more complicated, because there is a different F-distribution for every combination of the number of groups we are comparing and the total sample size. We will nevertheless say that for most situations, an F-statistic greater than 4 would be considered rather large, but tables or software are needed to get a truly accurate assessment.
Example

The parts of the output that we focus on here have been highlighted. In particular, note that the F-statistic is 46.60, which is very large, indicating that the data provide a lot of evidence against H0 (we can also see that the p-value is so small that it is essentially 0, which supports that conclusion as well).
Let’s move on to talk about the conditions under which we can safely use the ANOVA F-test, where the first two conditions are very similar to ones we’ve seen before, but there is a new third condition. It is safe to use the ANOVA procedure when the following conditions hold:
-
The samples drawn from each of the populations we’re comparing are independent.
-
The response variable varies normally within each of the populations we’re comparing. As you already know, in practice this is done by looking at the histograms of the samples and making sure that there is no evidence of extreme departure from normality in the form of extreme skewness and outliers. Another possibility is to look at side-by-side boxplots of the data, and add histograms if a more detailed view is necessary. For large sample sizes, we don’t really need to worry about normality, although it is always a good idea to look at the data.
-
The populations all have the same standard deviation. The best we can do to check this condition is to find the sample standard deviations of our samples and check whether they are “close.” A common rule of thumb is to check whether the ratio between the largest sample standard deviation and the smallest is less than 2. If that’s the case, this condition is considered to be satisfied.
Example
In our example all the conditions are satisfied:
-
All the samples were chosen randomly, and are therefore independent.
-
The sample sizes are large enough (n = 35) that we really don’t have to worry about the normality; however, let’s look at the data using side-by-side boxplots, just to get a sense of it:

You’ll recognize this plot as Scenario 2 from earlier. The data suggest that the frustration level of the business students is generally lower than students from the other three majors. The ANOVA F-test will tell us whether these differences are significant.
-
In order to use the rule of thumb, we need to get the sample standard deviations of our samples.
We can either calculate the standard deviation for each of the four samples by hand, or note that the variance for each sample appears in the Excel output and use that to calculate the standard deviation (remember that the square root of variance is standard deviation). Here, the standard deviation has been calculated and added to the output:

The rule of thumb is satisfied, since 3.082/2.088 < 2.
Did I get this?
In each of the following three questions, you’ll find two designs for comparing number of credits taken by freshmen versus sophomores versus juniors versus seniors. In each case, one of the designs should not be handled with ANOVA. Your task is to identify which of the two it is.
Step 3: Finding the p-value
The p-value of the ANOVA F-test is the probability of getting an F statistic as large as we got (or even larger), had [latex]H_{0}:\mu _{1}=\mu _{1}=...=\mu _{k}[/latex] been true. In other words, it tells us how surprising it is to find data like those observed, assuming that there is no difference among the population means μ1, μ2, …, μk.
Example
As we already noticed before, the p-value in our example is so small that it is essentially 0, telling us that it would be next to impossible to get data like those observed had the mean frustration level of the four majors been the same (as the null hypothesis claims).

Step 4: Making Conclusions in Context
As usual, we base our conclusion on the p-value. A small p-value tells us that our data contain a lot of evidence against Ho. More specifically, a small p-value tells us that the differences between the sample means are statistically significant (unlikely to have happened by chance), and therefore we reject Ho. If the p-value is not small, the data do not provide enough evidence to reject Ho, and so we continue to believe that it may be true. A significance level (cut-off probability) of .05 can help determine what is considered a small p-value.
Example
Before we give you hands-on practice in carrying out the ANOVA F-test, let’s look at another example:
Example
Do advertisers alter the reading level of their ads based on the target audience of the magazine they advertise in?
In 1981, a study of magazine advertisements was conducted (F.K. Shuptrine and D.D. McVicker, “Readability Levels of Magazine Ads,” Journal of Advertising Research, 21:5, October 1981). Researchers selected random samples of advertisements from each of three groups of magazines:
Group 1—highest educational level magazines (such as Scientific American, Fortune, The New Yorker)
Group 2—middle educational level magazines (such as Sports Illustrated, Newsweek, People)
Group 3—lowest educational level magazines (such as National Enquirer, Grit, True Confessions)
The measure that the researchers used to assess the level of the ads was the number of words in the ad. 18 ads were randomly selected from each of the magazine groups, and the number of words per ad were recorded.
The following figure summarizes this problem:

Our question of interest is whether the number of words in ads (Y) is related to the educational level of the magazine (X). To answer this question, we need to compare μ1,μ2,μ3, the mean number of words in ads of the three magazine groups. Note in the figure that the sample means are provided. It seems that what the data suggest makes sense; the magazines in group 1 have the largest number of words per ad (on average) followed by group 2, and then group 3.
The question is whether these differences between the sample means are significant. In other words, are the differences among the observed sample means due to true differences among the μ’s or merely due to sampling variability? To answer this question, we need to carry out the ANOVA F-test.
Step 1: Stating the hypotheses.
We are testing:

Conceptually, the null hypothesis claims that the number of words in ads is not related to the educational level of the magazine, and the alternative hypothesis claims that there is a relationship.
Step 2: Checking conditions and summarizing the data.
(i) The ads were selected at random from each magazine group, so the three samples are independent.
In order to check the next two conditions, we’ll need to look at the data (condition ii), and calculate the sample standard deviations of the three samples (condition iii). Here are the side-by-side boxplots of the data, followed by the standard deviations:


(ii) The graph does not display any alarming violations of the normality assumption. It seems like there is some skewness in groups 2 and 3, but not extremely so, and there are no outliers in the data.
(iii) We can assume that the equal standard deviation assumption is met since the rule of thumb is satisfied: the largest sample standard deviation of the three is 74 (group 1), the smallest one is 57.6 (group 3), and 74/57.6 < 2.
Before we move on, let’s look again at the graph. It is easy to see the trend of the sample means (indicated by red circles). However, there is so much variation within each of the groups that there is almost a complete overlap between the three boxplots, and the differences between the means are over-shadowed and seem like something that could have happened just by chance. Let’s move on and see whether the ANOVA F-test will support this observation.
Using statistical software to conduct the ANOVA F-test, we find that the Fstatistic is 1.18, which is not very large. We also find that the p-value is 0.317.
Step 3. Finding the p-value.
The p-value is 0.317, which tells us that getting data like those observed is not very surprising assuming that there are no differences between the three magazine groups with respect to the mean number of words in ads (which is what Ho claims).
In other words, the large p-value tells us that it is quite reasonable that the differences between the observed sample means could have happened just by chance (i.e., due to sampling variability) and not because of true differences between the means.
Step 4: Making conclusions in context.
The large p-value indicates that the results are not significant, and that we cannot reject Ho.
We therefore conclude that the study does not provide evidence that the mean number of words in ads is related to the educational level of the magazine. In other words, the study does not provide evidence that advertisers alter the reading level of their ads (as measured by the number of words) based on the educational level of the target audience of the magazine.
Final Comment
However, the ANOVA F-test does not provide any insight into why H0 was rejected; it does not tell us in what way μ1,μ2,μ3...,μk are not all equal. We would like to know which pairs of ’s are not equal. As an exploratory (or visual) aid to get that insight, we may take a look at the confidence intervals for group population meansμ1,μ2,μ3...,μk that appears in the output. More specifically, we should look at the position of the confidence intervals and overlap/no overlap between them.
* If the confidence interval for, say,μi overlaps with the confidence interval for μj , then μi and μj share some plausible values, which means that based on the data we have no evidence that these two ’s are different.

* If the confidence interval for μi does not overlap with the confidence interval for μj , then μi and μj do not share plausible values, which means that the data suggest that these two ’s are different.

Furthermore, if like in the figure above the confidence interval (set of plausible values) for μi lies entirely below the confidence interval (set of plausible values) for μj, then the data suggest that μi is smaller than μj.
Example
Consider our first example on the level of academic frustration.

Based on the small p-value, we rejected Ho and concluded that not all four frustration level means are equal, or in other words that frustration level is related to the student’s major. To get more insight into that relationship, we can look at the confidence intervals above (marked in red). The top confidence interval is the set of plausible values for μ 1, the mean frustration level of business students. The confidence interval below it is the set of plausible values for μ 2, the mean frustration level of English students, etc.
What we see is that the business confidence interval is way below the other three (it doesn’t overlap with any of them). The math confidence interval overlaps with both the English and the psychology confidence intervals; however, there is no overlap between the English and psychology confidence intervals.
This gives us the impression that the mean frustration level of business students is lower than the mean in the other three majors. Within the other three majors, we get the impression that the mean frustration of math students may not differ much from the mean of both English and psychology students, however the mean frustration of English students may be lower than the mean of psychology students.
Note that this is only an exploratory/visual way of getting an impression of why Ho was rejected, not a formal one. There is a formal way of doing it that is called “multiple comparisons,” which is beyond the scope of this course. An extension to this course will include this topic in the future.
Let’s summarize
- The ANOVA F-test is used for comparing more than two population means when the samples (drawn from each of the populations we are comparing) are independent. We encounter this situation when we want to examine the relationship between a quantitative response variable and a categorical explanatory variable that has more than two values.
- The hypotheses that are being tested in the ANOVA F-test are: H0 : μ1 = μ2=...= μk Ha: not all u’s are equal
- The idea behind the ANOVA F-test is to check whether the variation among the sample means is due to true differences among the μ’s or merely due to sampling variability by looking at: [latex]\frac{Variation\ among\ the\ sample\ means}{Variation\ within\ the\ groups}[/latex]
- Once we verify that we can safely proceed with the ANOVA F-test, we use software to carry it out.
- If the ANOVA F-test has rejected the null hypothesis we can look at the confidence intervals for the population means that are in the output to get a visual insight into why Ho was rejected (i.e., which of the means differ).