5.2: Discrete Random Variables
As the introduction suggests, the first part of this chapter will be devoted to discrete random variables: variables whose possible values are a list of distinct values. In order to decide on some notation, let’s look at the coin toss example again:
A fair coin is tossed twice. Let the random variable X be the number of tails we get in this random experiment. In this case, the possible values that X can assume are 0 (if we get HH), 1 (if get HT or TH) , and 2 (if we get TT).
Notation
If we want to find the probability of the event “getting 1 tail,” we’ll write: P(X = 1)
If we want to find the probability of the event “getting 0 tails,” we’ll write: P(X = 0)
In general, we’ll write: P(X = x) to denote the probability that the discrete random variable X gets the value x.
Note that for the random variables we’ll use a capital letter, and for the value we’ll use a lowercase letter.
Probability Distribution
When we learned how to find probabilities by applying the basic principles, we generally focused on just one particular outcome or event, like the probability of getting exactly one tail when a coin is tossed twice, or the probability of getting a 5 when a die is rolled. Now that we have mastered the solution of individual probability problems, we’ll proceed to look at the big picture by considering all the possible values of a discrete random variable, along with their associated probabilities. This list of possible values and probabilities is called the probability distribution of the random variable.
Comment
In the Exploratory Data Analysis unit of this course, we often looked at the distribution of sample values in a quantitative data set. We would display the values with a histogram, and summarize them by reporting their mean. In this section, when we look at the probability distribution of a random variable, we consider all its possible values and their overall probabilities of occurrence. Thus, we have in mind an entire population of values for a variable. When we display them with a histogram or summarize them with a mean, these are representing a population of values, not a sample. The distinction between sample and population is an essential concept in statistics, because an ultimate goal is to draw conclusions about unknown values for a population, based on what is observed in the sample.
Recall our first example, when we introduced the idea of a random variable. In this example we tossed a coin twice.
Example
Flipping a Coin Twice
What is the probability distribution of X, where the random variable X is the number of tails appearing in two tosses of a fair coin?
We first note that since the coin is fair, each of the four outcomes HH, HT, TH, TT in the sample space S is equally likely, and so each has a probability of 1/4. (Alternatively, the multiplication principle can be applied to find the probability of each outcome to be 1/2 * 1/2 = 1/4.)
X takes the value 0 only for the outcome HH, so the probability that X = 0 is 1/4.
X takes the value 1 for outcomes HT or TH. By the addition principle, the probability that X = 1 is 1/4 + 1/4 = 1/2.
Finally, X takes the value 2 only for the outcome TT, so the probability that X = 2 is 1/4.
The probability distribution of the random variable X is easily summarized in a table:
As mentioned before, we write “P(X = x)” to denote “the probability that the random variable X takes the value x.”
The way to interpret this table is:
X takes the values 0, 1, 2 and P(X = 0) = 1/4, P(X = 1) = 1/2, P(X = 2) = 1/4.
Note that events of the type (X = x) are subject to the principles of probability established earlier, and will provide us with a way of systematically exploring the behavior of random variables. In particular, the first two principles in the context of probability distributions of random variables will now be stated.
Any probability distribution of a discrete random variable must satisfy:
- [latex]0\le\mathcal{P}\left(\mathcal{X}-\mathcal{x}\right)\le1[/latex]
- [latex]\sum\mathcal{x}\mathcal{P}(\mathcal{X}=\mathcal{x})=1[/latex]
The probability distribution for two flips of a coin was simple enough to construct at once. For more complicated random experiments, it is common to first construct a table of all the outcomes in S and their probabilities, then use the addition principle to condense that information into the actual probability distribution table.
Example
Flipping a Coin Three Times
A coin is tossed three times. Let the random variable X be the number of tails. Find the probability distribution of X. We’ll follow the same reasoning we used in the previous example:
First, we specify the 8 possible outcomes in S, along with the number and the probability of that outcome. (Because they are all equally likely, each has probability 1/8. Alternatively, by the multiplication principle, each particular sequence of three coin faces has probability 1/2 * 1/2 * 1/2 = 1/8.)
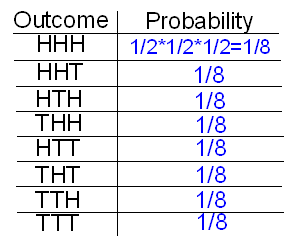
Next, we figure out what the value of X is (number of tails) for each possible outcome.
Next, we use the addition principle to assert that
P(X = 1) = P(HHT or HTH or THH) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8.
Similarly, P(X = 2) = P(HTT or THT or TTH) = 3/8.
The resulting probability distribution is:
The purpose of the next activity is to give you guided practice in finding the probability distribution of a discrete random variable.
Learn by Doing
In the previous two examples and activity, we needed to specify the probability distributions ourselves, based on the physical circumstances of the situation. In some situations, as in the following example, the probability distribution may be specified with an algebraic formula. Such a formula must be consistent with the constraints imposed by the laws of probability, so that the probability of each outcome must be between 0 and 1, and the probabilities of all possible outcomes together must sum to 1.
Example
Formulas to Define Random Variables
A random variable X has a probability distribution of
P(X = x) = (x + 2) / 25 for x = 1, 2, 3, 4, 5.
Show the probability distribution in a table, and verify that the above requirements are satisfied.
Substituting x = 1, 2, 3, 4, and 5, respectively, into the formula for P(X = x), we have
Clearly, each probability is between 0 and 1. Also, the probabilities sum to (3 + 4 + 5 + 6 + 7) / 25 = 25/25 = 1.
Did I get this?
The number of sales that a telemarketing salesperson makes in an hour is a random variable X having the following probability distribution:
Probability Histograms
We learned to display the distribution of sample values for a quantitative variable with a histogram in which the horizontal axis represented the range of values in the sample. The vertical axis represented the frequency or relative frequency (sometimes given as a percentage) of sample values occurring in that interval. So the width of each rectangle in the histogram was an interval, or part of the possible values for the quantitative variable, and the height of each rectangle was the frequency (or relative frequency) for that interval.
Similarly, we can display the probability distribution of a random variable with a probability histogram. The horizontal axis represents the range of all possible values of the random variable, and the vertical axis represents the probabilities of those values.
Here is the probability histogram for the previous example:
Area of a Probability Histogram
Notice that each rectangle in the histogram has a width of 1 unit. The height of each rectangle is the probability that it will occur. Thus, the area of each rectangle is base times height, which for these rectangles is 1 times its probability for each value of X. This means that the sum of the areas of all of the rectangles is the same as the sum of all of the probabilities. Therefore, the total area = 1.
Learn by Doing
Based upon data collected in the 2000 United States Census and an expanded number of households, the following histogram was constructed. It shows the distribution of people per household.
Did I get this?
The probability distribution of the random variable X is represented by the following histogram.
We’ve seen how probability distributions are created. Now it’s time to use them to find probabilities.
Example
Changing Majors
A random sample of graduating seniors was surveyed just before graduation. One question that was asked is: How many times did you change majors? The results are displayed in a probability distribution.
Using this probability distribution we can answer probability questions such as: What is the probability that a randomly selected senior has changed majors more than once? This can be written as P(X > 1).
More than once would be translated to:
| P(X > 1) | = | P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) |
| = | .23 + .09 + .02 + .01 | |
| = | .35 |
As you just saw in this example, we need to pay attention to the wording of the probability question. The key words that told us which values to use for X are more than. The following will clarify and reinforce the key words and their meanings.
Key Words
Let’s begin with some everyday situations using at least and at most.
Suppose someone said to you, “I need you to write at least 10 pages for a term paper.” What does this mean? It means that 10 pages is the smallest amount you are going to write. In other words, you will write 10 or more pages for the term paper. This would be the same as saying, “not less than 10 pages.” So, for example, writing 9 pages would be unacceptable.
On the other hand, suppose you are considering the number of children you will have. You want at most 3 children. This means that 3 children is the most that you wish to have. In other words, you will have 3 or fewer children. This would be the same as saying, “not more than 3 children.” So, for example, you would not want to have 4 children.
The following table gives a list of some key words to know. Suppose a random variable X had possible values of 0-5.
| Key Words | Meaning | Symbols | Values for X |
|---|---|---|---|
| more than 2 | strictly larger than 2 | X > 2 | 3, 4, 5 |
| no more than 2 | 2 or fewer | X ≤ 2 | 0, 1, 2 |
| fewer than 2 | strictly smaller than 2 | X < 2 | 0, 1 |
| no less than 2 | 2 or more | X ≥ 2 | 2, 3, 4, 5 |
| at least 2 | 2 or more | X ≥ 2 | 2, 3, 4, 5 |
| at most 2 | 2 or fewer | X ≤ 2 | 0, 1, 2 |
| exactly 2 | 2, no more or no less, only 2 | X = 2 | 2 |
Learn by Doing
A random variable X has possible values of 1-6.
Learn by Doing
Before we move on to the next section on the means and variances of a probability distribution, let’s revisit the changing majors example:
After we learn about means and standard deviations, we will have another way to answer these types of questions.
Here is another example in which we’ll use a probability distribution that is associated with a random variable of interest to find probabilities. What will be new in this example is the use of conditional probabilities.
Example
Xavier’s Production Line
The number of defective parts produced each hour by Xavier’s production line is a random variable X with the following probability distribution:
Using the probability distribution of a random variable, we can answer some probability questions:
[latex]\mathcal{P}\left(\mathcal{X}\geq2\right)=\mathcal{P}\left(\mathcal{X}=2\right)+\mathcal{P}\left(\mathcal{X}=3\right)+\mathcal{P}\left(\mathcal{X}=4\right)=0.25+0.20+0.10=0.55[/latex]
(Note that the addition principle has been applied.)
(b) Suppose it is known that more than 2 defects were produced in a particular hour. What is the probability that the number of defects was fewer than 4?
We use the conditional probabilities definition [latex]\mathcal{P}\left(\mathcal{B}\middle|\mathcal{A}\right)=\frac{\mathcal{P}\left(\mathcal{A}and\mathcal{B}\right)}{\mathcal{P}\left(\mathcal{A}\right)}[/latex] to solve: [latex]\mathcal{P}\left(\mathcal{X}<4\middle|\mathcal{X}>2\right)=\frac{\mathcal{P}\left(\left(\mathcal{X}<4\right)and\left(\mathcal{X}>2\right)\right)}{\mathcal{P}\left(\mathcal{X}>2\right)}=\frac{\mathcal{P}\left(\mathcal{X}=3\right)}{\mathcal{P}\left(\mathcal{X}>2\right)}=\frac{0.2}{0.3}=0.67[/latex]
Note that we are substituting the event “X < 4” for event B, and the event “X > 2” for event A.
Also note that the only way that (X < 4) and (X > 2) can happen together is if X = 3.
The purpose of the next activity is to give you guided practice at using the probability distribution of a random variable to find probabilities of interest.
Learn by Doing
Recall the following example:
The number of sales that a telemarketing salesperson makes in an hour is a random variable X having the following probability distribution:
Did I get this?
Data were collected from a survey given to graduating college seniors on the number of times they had changed majors. From that data, a probability distribution was constructed. The random variable X is defined as the number of times a graduating senior changed majors. It is shown below:
