2.1: Organizing and Visualizing Data

Organizing One Categorical Variable

What is your perception of your own body? Do you feel that you are overweight, underweight, or about right?

A random sample of 1,200 U.S. college students were asked this question as part of a larger survey. The following table shows part of the responses:

Body Image

Student

Body Image

student 25

overweight

student 26

about right

student 27

underweight

student 28

about right

student 29

about right

Here is some information that would be interesting to get from these data:

  • What percentage of the sampled students fall into each category?

  • How are students divided across the three body image categories? Are they equally divided? If not, do the percentages follow some other kind of pattern?

There is no way that we can answer these questions by looking at the raw data, which are in the form of a long list of 1,200 responses, and thus not very useful. However, both these questions will be easily answered once we summarize and look at the distribution of the variable Body Image (i.e., once we summarize how often each of the categories occurs).

In order to summarize the distribution of a categorical variable, we first create a table of the different values (categories) the variable takes, how many times each value occurs (count) and, more importantly, how often each value occurs (by converting the counts to percentages); this table is called a frequency distribution. Here is the frequency distribution for our example:

Body Image Distribution
 

category

Count

Percent

About right

855

 [latex]\left(\frac{855}{1200}\right)\times100=71.3%[/latex]

Overweight

235

 [latex]\left(\frac{235}{1200}\right)\times100=19.6%[/latex]

Underweight

110

 [latex]\left(\frac{110}{1200}\right)\times100=9.2%[/latex]

Total

n=1200

100%

In order to visualize the numerical summaries we’ve obtained, we need a graphical display. There are two simple graphical displays for visualizing the distribution of categorical data:

  1. The Pie Chart

    A pie chart of the distribution. Taking up 71.3% of the chart is the "about right" category, which is labeled with "about right (855, 71.3%)". Another 9.2% of the chart os occupied by the section labeled "underweight (110, 9.2%)", and taking up 19.6% of the chart is the area labeled "overweight (235, 19.6%)". In total the three sections fill up the entire pie, so they make up 100% of the chart, which represents the entirety of the data.

  2. The Bar Chart

    Two bar charts. Since these bar charts can only show one type of unit on the vertical axis, two are required, one to show counts and one to show percentages. The first bar chart shows counts on the vertical axis, from 0 to 900. The horizontal axis has 3 labels under 3 bars. The largest bar is labeled "about right" and is the largest. It extends from the 0 mark on the vertical axis to between the 800 and 900 mark. The second bar is labeled "overweight" and starts at the 0 mark and ends at about the 200 mark. The third bar is labeled "underweight" and starts at the 0 mark and ends between the 100 and 200 mark. The second bar chart is identical to the first one, except the vertical axis has been changed to Percent units, and goes from 0 to 70. The bars are the same as in the first chart.

Learn by Doing

Now that we have summarized the distribution of values in the Body Image variable, let’s go back and interpret the results in the context of the questions that we posed:

Now that we’ve interpreted the results, there are some other interesting questions that arise:

  • Can we reliably generalize our results to the entire population of interest and conclude that a similar distribution across body image categories exists among all U.S. college students? In particular, can we make such a generalization even though our sample consisted of only 1,200 students, which is a very small fraction of the entire population?

  • If we had separated our sample by gender and looked at males and females separately, would we have found a similar distribution across body image categories?

These are the types of questions that we will deal with in future sections of the course.

Comments

  1. While both the pie chart and the bar chart help us visualize the distribution of a categorical variable, the pie chart emphasizes how the different categories relate to the whole, and the bar chart emphasizes how the different categories compare with each other.

  2. A variation on the pie chart and bar chart that is very commonly used in the media is the pictogram. Here are two examples:

    A bar chart in which the bars have been replaced by rolls of unraveled toilet paper. The chart is titled "How we flush a public toilet" The first bar is labeled "Use shoe, 41%", the second bar is labeled "Act normally 30%", and the last bar is labeled "Paper towel 17%"

    Source: USA Today Snapshots and the Impulse Research for Northern Confidential Bathroom survey

    A pie chart made out of a slice of cucumber. The cucumber is on a fork, which in turn is over a dinner table. The pie chart is titled "How often are salads eaten (per week)". The pie chart shows 4 sections: Never (3%), Daily (13%), 2 or less (37%), 3-6 times (47%).

    Source: Market Facts for the Association of Dressings and Sauces

  3. Beware: Pictograms can be misleading. Consider the following pictogram:

    A chart in which three items are represented by the size of a fountain pen. The chart is labeled "No. 1 for the Money with Consumer Services Advertisers" The smallest pen is U.S. News $1,537,617. The second smallest pen is Newsweek $2,698,386. The largest pen is TIME $4,433,879.

    This graph is aimed at advertisers deciding where to spend their budgets, and clearly suggests that Time magazine attracts by far the largest amount of advertising spending. Are the differences really as dramatic as the graph suggests? If we look carefully at the numbers above the pens, we find that advertisers spend in Time only $4,433,879 / $2,698,386 = 1.64 times more than in Newsweek, and only $4,433,879 / $1,537,617 = 2.88 times more than in U.S. News. By looking at the pictogram, however, we get the impression that Time is much further ahead. Why? In order to magnify the picture without distorting it, we must increase both its height and width. As a result, the area of Time’s pen is 1.64 * 1.64 = 2.7 times larger than the Newsweek pen, and 2.88 * 2.88 = 8.3 times larger than the U.S. News pen. Our eyes capture the area of the pens rather than only the height, and so we are misled to think that Time is a bigger winner than it really is.

Learn by Doing

One Categorical Variable

Let’s Summarize

  • The distribution of a categorical variable is summarized using:

    • Graphical display: pie chart or bar chart, supplemented by

    • Numerical summaries: category counts and percentages.

  • A variation on pie charts and bar charts is the pictogram.

  • Pictograms can be misleading, so make sure to use a critical approach when interpreting the information the pictogram is trying to convey.

Organizing One Quantitative Variable

In the previous section, we explored the distribution of a categorical variable using graphs (pie chart, bar chart) supplemented by numerical measures (percent of observations in each category). In this section, we will explore the data collected from a quantitative variable, and learn how to describe and summarize the important features of its distribution. We will first learn how to display the distribution using graphs and then move on to discuss numerical measures.

To display data from one quantitative variable graphically, we can use either the histogram or the stem plot. (Another graph, the boxplot, will be mentioned later).

Idea

Break the range of values into intervals and count how many observations fall into each interval.

Example

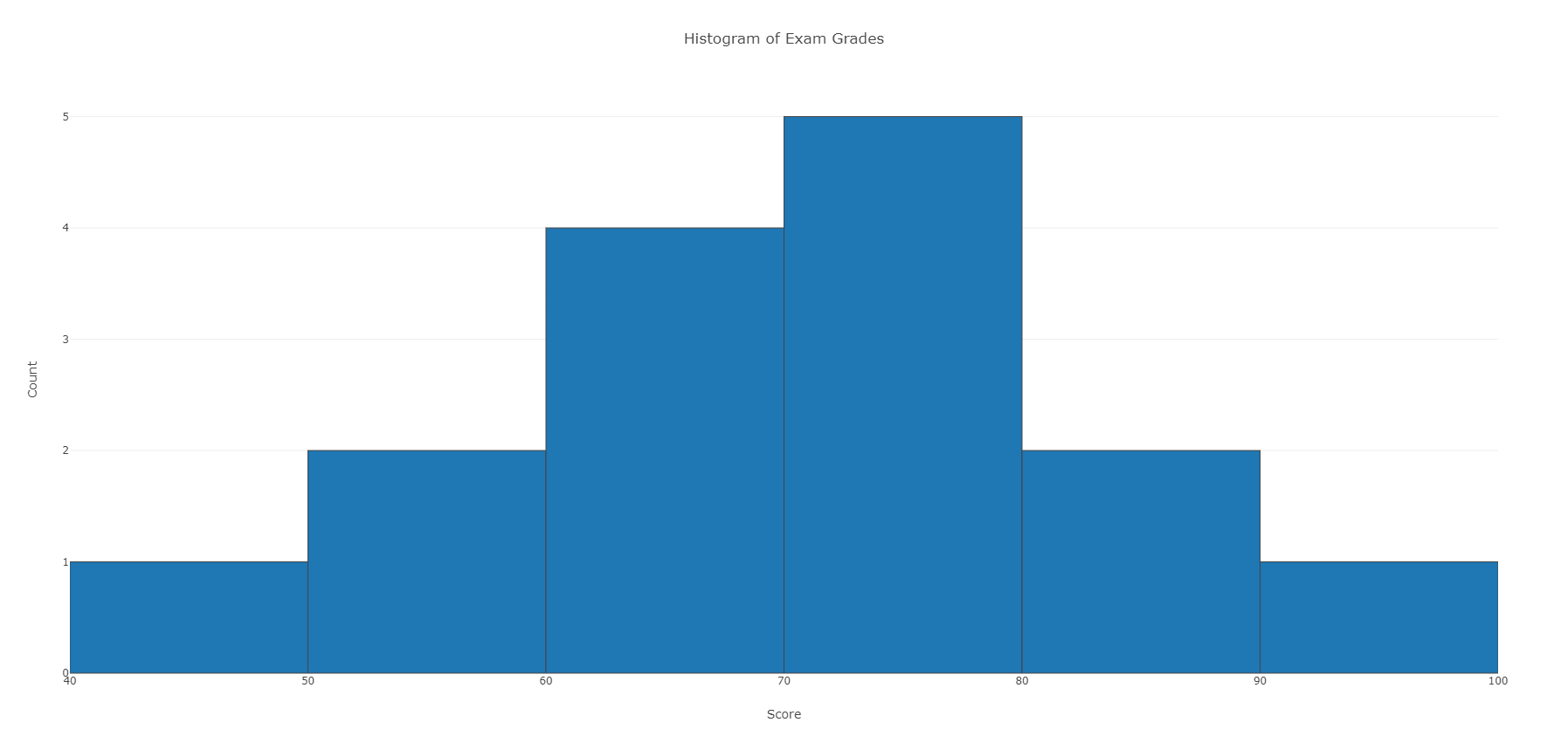
Exam Grades

Here are the exam grades of 15 students:

88, 48, 60, 51, 57, 85, 69, 75, 97, 72, 71, 79, 65, 63, 73

 

We first need to break the range of values into intervals (also called “bins” or “classes”). In this case, since our dataset consists of exam scores, it will make sense to choose intervals that typically correspond to the range of a letter grade, 10 points wide: 40–50, 50–60, … 90–100. By counting how many of the 15 observations fall in each of the intervals, we get the following table:

Exam Grades
Score Count
[40–50) 1
[50–60) 2
[60–70) 4
[70–80) 5
[80–90) 2
[90–100] 1

Note: The observation 60 was counted in the 60–70 interval. See comment 1 below.

To construct the histogram from this table we plot the intervals on the X-axis, and show the number of observations in each interval (frequency of the interval) on the Y-axis, which is represented by the height of a rectangle located above the interval:

The table above can also be turned into a relative frequency table using the following steps:

  1. Add a row on the bottom and include the total number of observations in the dataset that are represented in the table.
  2. Add a column, at the end of the table, and calculate the relative frequency for each interval, by dividing the number of observations in each row by the total number of observations.

These two steps are illustrated in red in the following frequency distribution table:

It is also possible to determine the number of scores for an interval, if you have the total number of observations and the relative frequency for that interval. For instance, suppose there are 15 scores (or observations) in a set of data and the relative frequency for an interval is .13. To determine the number of scores in that interval, multiplying the total number of observations by the relative frequency and round up to the next whole number: 15*.13 = 1.95, which rounds up to 2 observations.

A relative frequency table, like the one above, can be used to determine the frequency of scores occurring at or across intervals. Here are some examples, using the above frequency table:

  • What is the percentage of exam scores that were 70 and up to, but not including, 80?
    • To determine the answer, we look at the relative frequency associated with the [70-80) interval. The relative frequency is .33; to convert to percentage, multiply by 100 (.33*100= 33) or 33%.
  • What is the percentage of exam scores that are at least 70? To determine the answer, we need to:
    • Add together the relative frequencies for the intervals that have scores of at least 70 or above. Thus, would need to add together the relative frequencies from [70-80), [80-90), and [90-100] = .33+.13+.07 = .53.
    • To get the percentage, need to multiple the calculated relative frequency by 100. In this case, it would be .53*100 = 53 or 53%.

Learn by Doing

Here is the table from above, use it to answer the question.

Exam Grades
Score Count
[40–50) 1
[50–60) 2
[60–70) 4
[70–80) 5
[80–90) 2
[90–100] 1

Many students wonder…

Question: How do I know what interval width to choose?

Answer: There are no right or wrong choices of interval widths. In this course, we will rely on a statistical package to produce the histogram for us, and we will focus instead on describing and summarizing the distribution as it appears from the histogram.

Did I get this?

An instructor asked her students how much time (to the nearest hour) they spent studying for the midterm. The data are displayed in the following histogram:

histogram of time students spend studying

Did I get this?

Thirty-two students were asked the number of servings of fruits and vegetables they eat daily. The results are displayed in the histogram below.

histogram of fruit and vegetable consumption

Did I get this?

A survey was conducted to see how many phone calls people made daily. The results are displayed in the table below:

table of calls made daily

Interpreting the Histogram

Once the distribution has been displayed graphically, we can describe the overall pattern of the distribution and mention any striking deviations from that pattern. More specifically, we should consider the following features of the distribution:

The overall pattern of the distribution can be described by the shape, center, and spread of the histogram. Outliers in the distribution are deviations from the pattern.

We will get a sense of the overall pattern of the data from the histogram’s center, spread and shape, while outliers will highlight deviations from that pattern.

Distribution Shapes

When describing the shape of a distribution, we should consider:

  1. Symmetry/skewness of the distribution.

  2. Peakedness (modality)—the number of peaks (modes) the distribution has.

We distinguish between:

Symmetric Distributions

A symmetric, Single-peaked (Unimodal) distribution. The histogram's bars start at low values close to 0 on the left and rise to a peak where the x-axis is labeled 10. Then, the values decrease as we go right, back down to nearly 0.A symmetric, Double-peaked (Bimodal) distribution. The histogram's bars start at low values close to 0 on the left and rise to the first peak where the x-axis is labeled 10. Then, the values decrease as we go right, back down to nearly 0 at roughly where x=15. The values increase again and peak at x=20, and then, continuing right, decrease to nearly 0.A symmetric, Uniform distribution. Throughout the entire range of the x-axis the bars are roughly the same height, meaning they are the same value.

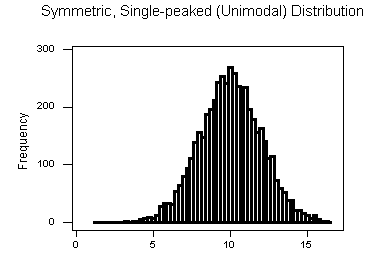
Note that all three distributions are symmetric, but are different in their modality (peakedness). The first distribution is unimodal—it has one mode (roughly at 10) around which the observations are concentrated. The second distribution is bimodal—it has two modes (roughly at 10 and 20) around which the observations are concentrated. The third distribution is kind of flat, or uniform. The distribution has no modes, or no value around which the observations are concentrated. Rather, we see that the observations are roughly uniformly distributed among the different values.

Skewed Right Distributions

A Skewed-right histogram. As we proceed from left to right across the x-axis, the bars rapidly increase to the peak of the histogram, located at roughly x=33. From there, the values slowly decrease, and the last measurement is at x=200. The bars of the histogram are barely visible above the x-axis starting at about x=150.

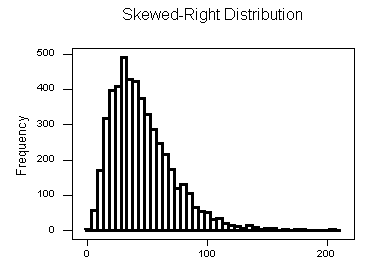
A distribution is called skewed right if, as in the histogram above, the right tail (larger values) is much longer than the left tail (small values). Note that in a skewed right distribution, the bulk of the observations are small/medium, with a few observations that are much larger than the rest. An example of a real-life variable that has a skewed right distribution is salary. Most people earn in the low/medium range of salaries, with a few exceptions (CEOs, professional athletes etc.) that are distributed along a large range (long “tail”) of higher values.

Skewed Left Distributions

A Skewed-Left histogram. As we proceed from left to right across the x-axis, the bars rapidly slowly to the peak of the histogram, located at roughly x=78. From there, the values rapidly decrease, and the last measurement is at x=90. Since the X-axis starts at 0, the peak is offset to the right of the center of the histogram.

A distribution is called skewed left if, as in the histogram above, the left tail (smaller values) is much longer than the right tail (larger values). Note that in a skewed left distribution, the bulk of the observations are medium/large, with a few observations that are much smaller than the rest. An example of a real life variable that has a skewed left distribution is age of death from natural causes (heart disease, cancer etc.). Most such deaths happen at older ages, with fewer cases happening at younger ages.

Comments

  1. Note that skewed distributions can also be bimodal. Here is an example. A medium size neighborhood 24-hour convenience store collected data from 537 customers on the amount of money spend in a single visit to the store. The following histogram displays the data.

    A histogram in which the Y-axis is labeled with units in Frequency, from 0 to 70. The X-axis is labeled in Dollars Spent, from 0 to 105. Going from left to right on the X-axis, the bars of the histogram increase to a peak at x=25, where y=70. Then, the bars decrease, but at x=45 they begin to increase again, reaching a second peak at x=50, where y=37. Then, the values decrease until the end of the histogram.

    Note that the overall shape of the distribution is skewed to the right with a clear mode around $25. In addition it has another (smaller) “peak” (mode) around $50-55. The majority of the customers spend around $25 but there is a cluster of customers who enter the store and spend around $50-55.

  2. If a distribution has more than two modes, we say that the distribution is multimodal.

Recall our grades example:

The exam grades histogram from earlier.

As you can see from the histogram, the grades distribution is roughly symmetric.

Center

The center of the distribution is its midpoint—the value that divides the distribution so that approximately half the observations take smaller values, and approximately half the observations take larger values. Note that from looking at the histogram we can get only a rough estimate for the center of the distribution. (More exact ways of finding measures of center will be discussed in the next section.)

Recall our grades example:

The exam grades histogram. The y-axis is labeled count, and the x-axis is labeled score. There is 1 count in 40-50 score interval, 2 counts in the 50-60 score interval, 4 counts in the 60-70 score interval, 5 counts in the 70-80 score interval, 2 counts in the 80-90 score interval, and 1 count in the 90-100 score interval.

As you can see from the histogram, the center of the grades distribution is roughly 70 (7 students scored below 70, and 8 students scored above 70).

Spread

The spread (also called variability) of the distribution can be described by the approximate range covered by the data. From looking at the histogram, we can approximate the smallest observation (min), and the largest observation (max), and thus approximate the range. (More exact ways of finding measures of spread are discussed in the next section.)

In our example:

Approximate min:

45 (the middle of the lowest interval of scores)

Approximate max:

95 (the middle of the highest interval of scores)

Approximate range:

95 − 45 = 50

Outliers

Outliers are observations that fall outside the overall pattern. For example, the following histogram represents a distribution that has a high probable outlier:

A histogram with frequency on the Y-axis. As we go from left to right on the x-axis, the frequency increases to a peak at x=5, then decreases. Eventually, we reach 0 at x=11. All of x > 10 have a frequency of 0, exception for x=15, which has a frequency of greater than zero. This is a outlier.

Go back and check the histogram of scores at the top of this page. As you can see, there are no outliers.

Example

Best Actress Oscar Winners

To provide an example of a histogram applied to actual data, we will look at the ages of Best Actress Oscar winners from 1970 to 2013 (To see the full dataset, click here.)

Review the histogram for the data.

We will now summarize the main features of the distribution of ages as it appears from the histogram:

Shape: The distribution of ages is skewed right. We have a concentration of data among the younger ages and a long tail to the right. The vast majority of the “best actress” awards are given to young actresses, with very few awards given to actresses who are older.

Center: The data seem to be centered around 34 or 35 years old. Note that this implies that roughly half the awards are given to actresses who are less than 34 years old.

Spread: The data range from about 20 to about 80, so the approximate range equals 80 – 20 = 60.

Outliers: There seem to be two probable outliers to the far right and possibly three around 62 years old.

You can see how informative it is to know “what to look at” in a histogram. If there is one conclusion that we can make here, it is that Hollywood likes to give Oscars to young actresses.

Learn by Doing

Histogram

Did I get this?

Did you get it?

If so, then go ahead and move on. If not, then click the link below for some additional practice.

Histogram (3 of 3): Extra Problems

Let’s Summarize

  • The histogram is a graphical display of the distribution of a quantitative variable. It plots the number (count) of observations that fall in intervals of values.

  • When examining the distribution of a quantitative variable, one should describe the overall pattern of the data (shape, center, spread), and any deviations from the pattern (outliers).

  • When describing the shape of a distribution, one should consider:

    • Symmetry/skewness of the distribution

    • Peakedness (modality)—the number of peaks (modes) the distribution has.

    *Not all distributions have a simple, recognizable shape.

  • Outliers are data points that fall outside the overall pattern of the distribution and need further research before continuing the analysis.

  • It is always important to interpret what the features of the distribution (as they appear in the histogram) mean in the context of the data.

Stemplot

The stem plot (also called stem and leaf plot) is another graphical display of the distribution of quantitative data.

Idea

Separate each data point into a stem and leaf, as follows:

The leaf is the right-most digit.

The stem is everything except the right-most digit.

So, if the data point is 34, then 3 is the stem and 4 is the leaf.

If the data point is 3.41, then 3.4 is the stem and 1 is the leaf.

Example

Best Actress Oscar Winners

We will continue with the Best Actress Oscar winners example (To see the full dataset, click here.)

34 34 27 37 42 41 36 32 41 33 31 74 33 49 38 61 21 41 26 80 42 29 33 36 45 49 39 34 26 25 33 35 35 28 30 29 61 32 33 45 29 62 22 44

To make a stem plot:

  1. Separate each observation into a stem and a leaf.

  2. Write the stems in a vertical column with the smallest at the top, and draw a vertical line at the right of this column.

  3. Go through the data points, and write each leaf in the row to the right of its stem.

  4. Rearrange the leaves in an increasing order.

The result of steps 1, 2, and 3 on the given data set results in the following: first row: 2|7169658992 second row: 3|3376231383694355023 third row: 4|2119124954 fourth row: 5| fifth row: 6|112 sixth row: 7|4 seventh row: 8|0 Step 4 results in: first row: 2|1256678999 second row: 3|0122333333445566789 third row: 4|1112244599 fourth row: 5| fifth row: 6|112 sixth row: 7|4 seventh row: 8|0 Following the extra step(*): first row: 2|12 second row: 2|56678999 third row: 3|012233333344 fourth row: 3|5566789 fifth row: 4|1112244 sixth row: 4|599 seventh row: 5| eighth row: 5| ninth row: 6|112 tenth row: 7|4 eleventh row:7| twelfth row: 8|0

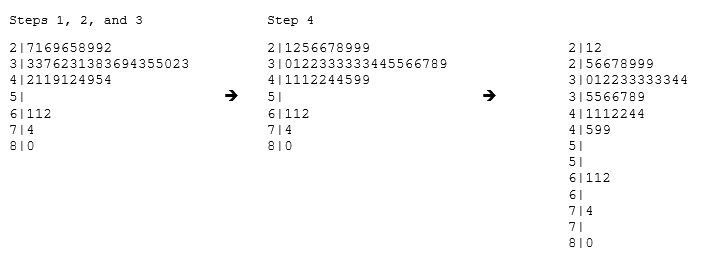
* When some of the stems hold a large number of leaves, we can split each stem into two: one holding the leaves 0-4, and the other holding the leaves 5-9. A statistical software package will often do the splitting for you, when appropriate.

Note that when rotated 90 degrees counterclockwise, the stem plot visually resembles a histogram:

A rotated stem plot. This is the same as the last stem plot given in the previous image, but rotated so that the stems are at the bottom, with the leaves on top.

This orientation makes the right-skewedness of the distribution clearly visible.

The stem plot has additional unique features:

  • It preserves the original data.

  • It sorts the data (which will become very useful in the next section).

Comment

There is another type of display that we can use to summarize a quantitative variable graphically—the dot plot. The dot plot, like the stem plot, shows each observation, but displays it with a dot rather than with its actual value. Here is the dot plot for the ages of Best Actress Oscar winners.

A dotplot titled "Dotplot of Age" A number line is at the bottom of the image, labeled in units of age from 24 to 80. At each age on the number line the a line of dots, each representing one winner of that age, appears above the place of that age on the number line.

Let’s Summarize

The stem plot is a simple but useful visual display of quantitative data. Its principal virtues are:

  • Easy and quick to construct for small, simple datasets.

  • Retains the actual data.

  • Sorts (ranks) the data.

Many students wonder…

Question: How do we know which graph to use: the histogram, stemplot, or dotplot?

Answer: Since for the most part we are not going to deal with very small data sets in this course, we will generally display the distribution of a quantitative variable using a histogram generated by a statistical software package.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Intro to Statistics MAT1260 by SBCCOE is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book